Читать книгу - "Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир"
Открой для себя врата в удивительный мир Читать книги / Домашняя книг на сайте books-lib.com! Здесь, в самой лучшей библиотеке мира, ты найдешь сокровища слова и истории, которые творят чудеса. Возьми свой любимый гаджет (Смартфоны, Планшеты, Ноутбуки, Компьютеры, Электронные книги (e-book readers), Другие поддерживаемые устройства) и погрузись в магию чтения книги 'Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир' автора Джон Дербишир прямо сейчас – дарим тебе возможность читать онлайн бесплатно и неограниченно!
665 0 08:43, 26-05-2019Аннотация к книге "Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир", которую можно читать онлайн бесплатно без регистрации
• Бесконечно много этих чисел делится на 3; бесконечно много не делится.
• Бесконечно много из них больше чем 11; только четыре числа не больше.
• Бесконечно много из них представимы в виде суммы двух простых; нет таких, которые не представимы — гипотеза Гольдбаха (которая все еще не доказана на момент написания книги).
Статья Литлвуда, также опубликованная в Comptes Rendus Парижской академии наук в том же году, называлась Sur la distribution des nombres premiers. В ней доказан результат столь же тонкий и столь же замечательный, как результат Харди, хотя и относящийся к несколько другому направлению исследований в данной области. Обсуждение этого результата требует небольшой преамбулы.
VI.
Мы уже отмечали, что в начале XX века наблюдалось следующее общее направление мыслей по поводу Гипотезы Римана. Теорема о распределении простых чисел (ТРПЧ) была доказана. С математической точностью было установлено, что действительно π(x) ~ Li(x) — или, словами, что относительная разность между π(x) и Li(x) уменьшается до нуля по мере того, как x делается все больше и больше. Так что же тогда можно утверждать об этой разности — т.е. об остаточном члене? Именно при внимательном рассмотрении остаточного члена математики обратили свои взоры к Гипотезе Римана, поскольку в работе Римана 1859 года для остаточного члена было приведено точное выражение. Как будет показано в должном месте, это выражение включает в себя все нетривиальные нули дзета-функции, так что ключ к пониманию остаточного члена каким-то образом скрыт среди этих нулей.
Чтобы говорить более конкретно, я приведу некоторые реальные значения остаточного члена. В таблице 14.1 «абсолютн.» означает разность Li(x) − π(x), а «относит.» означает это же число, отнесенное к (т.е. деленное на) π(x).
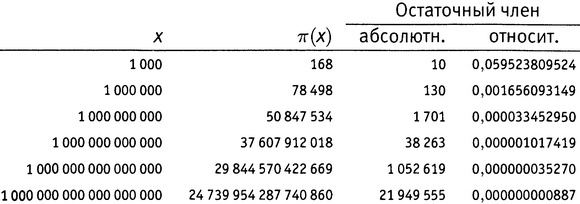
Таблица 14.1.
Мы видим, что относительная ошибка, без сомнения, уменьшается, стремясь к нулю, как ей и предписывает ТРПЧ. Это происходит потому что, хотя абсолютная ошибка тоже растет, она делает это далеко не так быстро, как π(x).
Пытливый математический ум сейчас спросит: «А как именно ведут себя эти два числа?» Имеются ли правила, описывающие медленный рост абсолютной ошибки или стремление относительной ошибки к нулю? Другими словами, если выкинуть из таблицы 14.1 вторую и четвертую колонки и рассмотреть получившуюся двухколоночную таблицу как «моментальный снимок» некоторой функции (колонки аргумент-значение), то что это будет за функция? Можно ли для нее получить формулу с волнами, как это было сделано для π(x)?
Здесь-то на сцене и появляются нетривиальные нули дзета-функции. Они тесно связаны (способом, который мы рассмотрим ниже во всех математических подробностях) с остаточным членом.
Хотя в ТРПЧ говорится об относительной ошибке, исследования в этой области в большей степени имеют дело с абсолютной ошибкой. На самом деле неважно, какую из них рассматривать. Относительная ошибка есть просто абсолютная ошибка, деленная на π(x), так что в любой момент несложно перейти от одной к другой. Итак, можно ли получить какие-нибудь результаты об абсолютном остаточном члене Li(x) − π(x)?
VII.
Взглянув на рисунок 7.6 и таблицу 14.1, можно с достаточной уверенностью заключить, что абсолютная разность Li(x) − π(x) положительна и возрастает. Численные свидетельства в пользу этого так убедительны, что Гаусс в своих собственных исследованиях полагал, что всегда так и происходит. Весьма вероятно, что исследователи поначалу соглашались с тем, или, по крайней мере, чувствовали уверенность в том, что π(x) всегда меньше чем Li(x). (Относительно мнения Римана по этому поводу ясности нет.) Поэтому статья Литлвуда 1914 года оказалась сенсацией, ибо в ней было установлено, что, напротив, существуют такие числа x, что π(x) больше чем Li(x). На самом деле доказано было гораздо большее.
Результат Литлвуда 1914 года
Разность Li(x) − π(x) изменяется от положительной к отрицательной и обратно бесконечно много раз.
Если учесть, что π(x) меньше, чем Li(x), для всех x, до которых смогли добраться даже самые мощные компьютеры, то где же находится первая точка перехода, первое «литлвудово нарушение», когда π(x) становится равной, а затем и превосходит Li(x)?
В подобных ситуациях математики отправляются на поиски того, что они называют верхней границей, — такого числа N, для которого можно доказать, что, каким бы ни был точный ответ на данный вопрос, он во всяком случае будет меньше, чем N. Установленные верхние границы такого рода нередко оказываются много больше, чем реальный ответ[131].
Так и обстояло дело с первой установленной верхней границей литлвудова нарушения. В 1933 году студент Литлвуда Сэмюель Скьюз показал, что если Гипотеза Римана верна, то переход должен наступать раньше, чем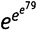
, что представляет собой число из примерно 10десять миллиардов триллионов триллионов цифр. Это не само число — это число цифр в том числе. (Для сравнения заметим, что общее количество всех атомов во Вселенной оценивается числом из примерно восьмидесяти цифр.) Этот монстр получил известность как «число Скьюза» — самое большое число, которое когда-либо до того следовало из математического доказательства.[132]
В 1955 году Скьюз улучшил свой результат, на этот раз даже не предполагая справедливости Гипотезы Римана, и оказалось, что новое число содержит 10одна тысяча цифр. В 1966 году Шерман Леман сумел понизить верхнюю границу до куда более разумного (по крайней мере, позволяющего себя записать) числа 1,165×101165 (числа, другими словами, из каких-то 1166 цифр), а потом еще сильнее, до 6,658×10370.
Прочитали книгу? Предлагаем вам поделится своим впечатлением! Ваш отзыв будет полезен читателям, которые еще только собираются познакомиться с произведением.
Оставить комментарий
-
Гость Елена12 июнь 19:12
Потрясающий роман , очень интересно. Обожаю Анну Джейн спасибо 💗
Поклонник - Анна Джейн
-
Гость24 май 20:12
Супер! Читайте, не пожалеете
Правила нежных предательств - Инга Максимовская
-
Гость Наталья21 май 03:36
Талантливо и интересно написано. И сюжет не банальный, и слог отличный. А самое главное -любовная линия без слащавости и тошнотного романтизма.
Вторая попытка леди Тейл 2 - Мстислава Черная
-
Гость Владимир23 март 20:08
Динамичный и захватывающий военный роман, который мастерски сочетает драматизм событий и напряжённые боевые сцены, погружая в атмосферу героизма и мужества.
Боевой сплав - Сергей Иванович Зверев