Читать книгу - "Как не ошибаться. Сила математического мышления - Джордан Элленберг"

Если ваше знакомство с математикой ограничивается школьной программой, это означает, что вам известна весьма ограниченная, а в какой-то степени даже ложная версия этого предмета. Школьная математика состоит главным образом из совокупности фактов и правил – фактов, которые нельзя оспаривать, и правил, которые предписаны высшим авторитетом и не подлежат сомнению. Такой подход рассматривает математические концепции как нечто непреложное.

Но математика не неизменна. Даже если речь идет о базовых объектах изучения, таких как числа и геометрические фигуры, наше незнание гораздо больше знания. А то, что мы все же знаем, получено в результате огромных усилий, разногласий и недоразумений. Весь этот труд и смятение тщательно завуалированы в ваших учебниках.

Безусловно, факты фактам рознь. Никогда не было особых споров по поводу того, что 1 + 2 = 3. Но можем ли мы действительно доказать, что 1 + 2 = 3, и как это можно сделать, – вопрос, который блуждает где-то между математикой и философией. Однако это совсем другая история, и мы вернемся к ней в конце книги. Правильность вычислений в данном случае не подлежит сомнению. Проблема кроется совсем в другом. Мы не раз столкнемся с ней на этих страницах.

Математические факты могут быть простыми и сложными, поверхностными и глубокими, что делит математическую вселенную на четыре сектора:

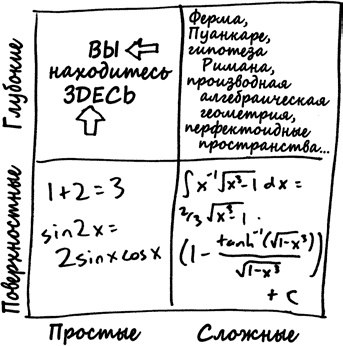
Базовые арифметические факты, такие как 1 + 2 = 3, относятся к категории простых и поверхностных. К этой же категории принадлежат и основные тождества, в частности sin(2x) = 2sin x × cos x или формула корней квадратного уравнения. Возможно, убедить себя в истинности таких тождеств немного труднее, чем в том, что 1 + 2 = 3, но по большому счету они не так уж сложны на концептуальном уровне.

В сегменте сложных и поверхностных фактов находится, например, задача умножения двух десятизначных чисел, или вычисление сложного определенного интеграла, или (при условии, что вы пару лет учились в магистратуре) определение следа Фробениуса на модулярной форме кондуктора 2377. Можно предположить, что по какой-то причине вам понадобится найти ответ на вопрос такого рода, но поиск решения вручную, вне всяких сомнений, покажется слишком раздражающей и невыполнимой задачей. В случае модулярной формы вам, возможно, понадобится серьезное образование даже для того, чтобы понять, о чем идет речь. Однако в действительности знание этих ответов не обогащает понимание окружающего мира.

Сектор сложных и глубоких математических фактов – это именно то, на что тратят большую часть своего времени профессиональные математики, к числу которых отношусь и я. Здесь обитают знаменитые теоремы и гипотезы, такие как гипотеза Римана, последняя теорема Ферма^[14], гипотеза Пуанкаре^[15], равенство классов P и NP^[16], теорема Гёделя и так далее. Каждая из этих теорем касается идей, имеющих глубокий смысл, фундаментальную важность, поразительную красоту и сугубо специальный характер, и каждая из них сама по себе выступает в качестве главного персонажа многих книг^{12}.

Но только не моей. То, о чем пойдет речь в настоящей книге, относится к верхнему левому сектору, где находятся простые и глубокие факты. Вы сможете непосредственно, с выгодой для себя использовать представленные здесь математические идеи независимо от того, ограничивается ли ваше математическое образование основами алгебры или охватывает гораздо более широкую область математики. И речь идет не о «фактах самих по себе», таких как простые арифметические утверждения, а о принципах, применение которых выходит далеко за рамки привычных представлений о математике. Мы будем говорить о надежных практических инструментах – их применение поможет вам не совершать ошибок.

Чистая математика представляется чем-то вроде монастыря – спокойное место, надежно защищенное от влияния окружающего мира со всей его суетой и противоречиями. Я вырос в стенах такого убежища. Знакомых мне математически одаренных молодых людей интересовало практическое применение математики в физике или геномике, многих влекла черная магия управления хедж-фондами, но все эти подростковые шатания и проблемы выбора были не для меня^[17]. Во время учебы в магистратуре я посвятил себя изучению теории чисел, которую Гаусс называл «королевой математики». Из всех чистых дисциплин это была самая чистейшая – закрытый сад посреди монастыря, где мы размышляли над теми же вопросами о числах и уравнениях, которые занимали умы древних греков и которые едва ли стали менее мучительными за прошедшие две с половиной тысячи лет.