Читать книгу - "Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир"
Аннотация к книге "Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир", которую можно читать онлайн бесплатно без регистрации
| z | z2 |
|---|---|
| −4 + 7i | −33 − 56i |
| 1 + i | 2i |
| i | −1 |
| 0,174 − 1,083i | −1,143 − 0,377i |
Таблица 13.1. Функция возведения в квадрат.
Читателю, возможно, нелегко в это поверить, но изучение «функций комплексной переменной» представляет собой одно из наиболее элегантных и прекрасных направлений в высшей математике. Области определения всех функций, знакомых нам из школьной математики, легко расширяются на все, или почти все, комплексные числа. Например, в таблице 13.2 приведен «моментальный снимок» показательной функции для некоторых комплексных чисел.
| z | ez |
|---|---|
| −1 + 2,141593i | −0,198766 + 0,30956i |
| 3,141593i | −1 |
| 1 + 4,141593i | −1,46869 − 2,28736i |
| 2 + 5,141593i | 3,07493 − 6,71885i |
| 3 + 6,141593i | 19,885 − 2,83447i |
Таблица 13.2. Показательная функция.
Заметим, что, как и ранее, когда мы увеличивали аргументы «по сложению» — а сейчас, разумеется, дело обстоит таким же образом, поскольку к аргументу каждый раз прибавляется 1 + i, — значения функции изменяются «по умножению», в данном случае за счет умножения на 1,46869 + 2.28736i. Если бы мы взяли аргументы, отличающиеся друг от друга прибавлением каждый раз числа 1, то, конечно, получающиеся значения отличались бы умножением на e. Заметим еще, что в эту таблицу включено одно из самых прекрасных тождеств во всей математике:
Говорят — и я полагаю, что такое вполне могло быть, — Гаусс утверждал, что если истинность этого выражения не становится для вас очевидной сразу же, при первом взгляде на него, то вы никогда не станете первоклассным математиком.
Но как же вообще можно определить комплексную степень числа e, как, впрочем, и любого другого числа? С помощью ряда, вот как. Следующее выражение дает реальное определение того, что такое ez для вообще любого числа z, будь оно вещественным или комплексным (13.1):
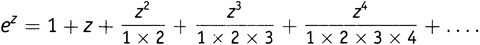
Чудесным (как мне представляется) образом эта бесконечная сумма сходится для любого числа z. Знаменатели растут так быстро, что рано или поздно побеждают любую степень любого числа. Равным образом чудесно, что если z — натуральное число, то бесконечная сумма оказывается в точности равной тому, что мы ожидаем от определения «степени» в обычном смысле, хотя разглядывание выражения (13.1) и не дает никаких намеков на то, почему бы такое могло случиться. Если z равно 4, то этот ряд оказывается равным в точности тому же, чему равно e×e×e×e (что, собственно, и понимается под обозначением e4).
Давайте просто подставим πi в выражение (13.1) и посмотрим, как быстро оно сходится. Если z равно πi, то z2 равно −π2; z3 равно −π3i; z4 равно π4; z5 равно π5i и т.д. Подставляя эти значения в бесконечную сумму и вычисляя возникающие степени числа π (для простоты с точностью до шести знаков после запятой), получаем сумму
Если сложить первые 10 из этих членов, то получим −1,001829104 + 0,006925270i. Если сложить первые 20 чисел, то результат будет равен −0,9999999999243491 − 0,000000000528919i. Вполне определенным образом сумма сходится к −1. Вещественная часть приближается к −1, а мнимая исчезает.
Можно ли и логарифмическую функцию продолжить на комплексные числа? Да. И получится, разумеется, в точности функция, обратная к показательной. Если ez = w, то z = ln w. К сожалению, как и в случае квадратных корней, если мы не соблюдем меры предосторожности, мы тут же попадем в зыбучие пески многозначных функций. Это происходит из-за того, что в комплексном мире показательная функция иногда принимает одно и то же значение при различных аргументах. Например, куб числа −1, в соответствии с правилом знаков, есть −1; так что возведение в куб обеих частей равенства eπi = −1 дает e3πi = −1; таким образом, аргументы πi и 3πi дают одно и то же значение функции, равное −1, подобно тому как −2 и +2 дают при возведении в квадрат одно и то же значение 4. Тогда что же такое ln (−1)? Это πi? Или же 3πi?
Это πi. Чтобы не наживать лишних неприятностей, ограничим мнимую часть значений функции отрезком от −π (не включая) до π (включая). Тогда для всякого ненулевого комплексного числа имеется его логарифм, причем ln (−1) = πi. На самом деле, если использовать обозначения, введенные в главе 11.v, то ln z = ln |z| + iΦ(z), где Φ(z), разумеется, измеряется в радианах. В таблице 13.3 показан «моментальный снимок» логарифмической функции с точностью до шести знаков после запятой. Аргументы здесь изменяются «по умножению» (каждая строка получается умножением 1 + i на предыдущую строку), а значения функции — «по сложению» (всякий раз прибавляется 0,346574 + 0,785398i).
Прочитали книгу? Предлагаем вам поделится своим впечатлением! Ваш отзыв будет полезен читателям, которые еще только собираются познакомиться с произведением.
Оставить комментарий
-
 Илья12 январь 15:30
Книга прекрасная особенно потому что Ее дали в полном виде а не в отрывке
Горький пепел - Ирина Котова
Илья12 январь 15:30
Книга прекрасная особенно потому что Ее дали в полном виде а не в отрывке
Горький пепел - Ирина Котова
-
 Гость Алексей04 январь 19:45
По фрагменту нечего комментировать.
Бригадный генерал. Плацдарм для одиночки - Макс Глебов
Гость Алексей04 январь 19:45
По фрагменту нечего комментировать.
Бригадный генерал. Плацдарм для одиночки - Макс Глебов
-
 Гость галина01 январь 18:22
Очень интересная книга. Читаю с удовольствием, не отрываясь. Спасибо! А где продолжение? Интересно же знать, а что дальше?
Чужой мир 3. Игры с хищниками - Альбер Торш
Гость галина01 январь 18:22
Очень интересная книга. Читаю с удовольствием, не отрываясь. Спасибо! А где продолжение? Интересно же знать, а что дальше?
Чужой мир 3. Игры с хищниками - Альбер Торш
-
 Олена кам22 декабрь 06:54
Слушаю по порядку эту серию книг про Дашу Васильеву. Мне очень нравится. Но вот уже третий день захожу, нажимаю на треугольник и ничего не происходит. Не включается
Донцова Дарья - Дантисты тоже плачут
Олена кам22 декабрь 06:54
Слушаю по порядку эту серию книг про Дашу Васильеву. Мне очень нравится. Но вот уже третий день захожу, нажимаю на треугольник и ничего не происходит. Не включается
Донцова Дарья - Дантисты тоже плачут





