Читать книгу - "Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир"

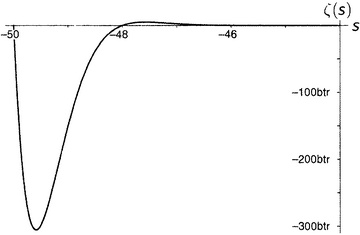
Рисунок 9.10.

V.

Ho как я получил все эти значения ζ(s) для s, меньших 1? Мы уже видели, что бесконечный ряд из выражения (9.1) для этого непригоден. А что пригодно? Если бы ради спасения своей жизни мне пришлось вычислить значение ζ(−7,5), как бы я к этому подступился?

Я не могу объяснить этого в полной мере, потому что такое объяснение требует слишком значительного погружения в математический анализ. Но я попробую передать общую идею. Сначала определим некоторую новую функцию, используя бесконечный ряд, слегка отличный от ряда в выражении (9.1). Это η-функция; η (читается «эта») — седьмая буква греческого алфавита. Определим η-функцию как

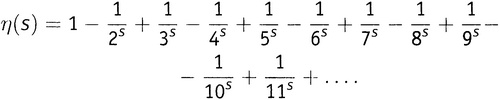
Грубая прикидка подсказывает, что у этой функции перспективы сходимости лучше, чем у выражения (9.1). Вместо непрестанного прибавления чисел здесь мы по очереди то прибавляем, то вычитаем, так что каждое следующее число до некоторой степени сокращает вклад предыдущего. Так оно и выходит. Математики в состоянии доказать — хотя здесь мы этим заниматься не будем, — что этот новый бесконечный ряд сходится всегда, когда s больше нуля. Это существенное улучшение по сравнению с выражением (9.1), которое сходится, только когда s больше единицы.

Но какая нам от всего этого польза в отношении дзета-функции? Для начала заметим, что в силу элементарных алгебраических правил A − B + C − D + E − F + G − H + … равно (A + B + C + D + E + F + G + H + …) минус 2×(B + D + F + H + …). Поэтому функцию η(s) можно переписать как

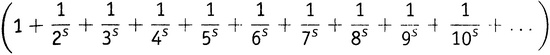
минус

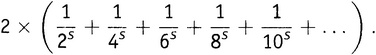
Первая скобка — это, конечно, ζ(s). Вторую скобку легко упростить, пользуясь 7-м правилом действий со степенями: (ab)ⁿ = aⁿbⁿ. Таким же образом каждое из этих четных чисел можно разбить в произведение вида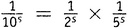, после чего можно вынести 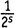в качестве множителя перед всей скобкой. А что останется в скобке? Там останется ζ(s)! Коротко говоря,

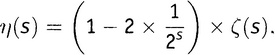
или, переписав это «наоборот» и слегка причесав, получаем

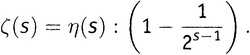
Вот. Это означает, что если нам удастся узнать какое-то значение η(s), то мы немедленно будем знать и значение ζ(s). А поскольку можно узнать значения η(s) между 0 и 1, можно получить и значение ζ(s) в этом промежутке, несмотря на то что «официальный» ряд для ζ(s) там не сходится.

Пусть, например, s равно ¹/₂. Если сложить 100 членов ряда для η(¹/₂), то получится 0,555023639…; если сложить 10 000 членов, получится 0,599898768…. В действительности значение η(¹/₂) составляет 0,604898643421630370…. (Существуют определенные приемы позволяющие вычислять такое без необходимости сложения мириад членов.) Вооруженные всем этим, мы можем вычислить значение ζ(¹/₂) оно оказывается равным −1,460354508…, что выглядит очень правдоподобно, если судить по первому графику из приведенного выше набора.

Но задержимся на мгновение. Не устроили ли мы тут игру в наперстки с двумя бесконечными рядами, один из которых сходится при аргументе s = ¹/₂, а другой — нет? Ну, строго говоря, мы действуем не совсем по правилам, и я обошелся довольно безответственно с той математикой, на которой здесь все основано. Однако же я получил правильный ответ, причем этот фокус можно повторить для любого числа между нулем и единицей (не включая ее) и получить правильное значение для ζ(s).

VI.

За исключением одного только s = 1, где ζ(s) не имеет значения, мы можем теперь предъявить значение дзета-функции для любого числа s, большего нуля. А как насчет аргументов равных нулю или меньших нуля? Вот здесь все по-настоящему круто. Один из результатов в работе Римана 1859 года состоит в доказательстве формулы, впервые предложенной Эйлером в 1749 году, которая выражает ζ(1 − s) через ζ(s). Таким образом, если мы желаем узнать, например, значение ζ(−15), то надо просто вычислить значение ζ(16) и подставить его в эту формулу. Это, правда, неслабая формула, и я привожу ее главным образом для полноты картин:^[75]

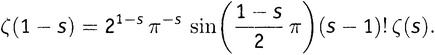
Всюду здесь π — это магическое число 3,14159265…, sin — добрая старая тригонометрическая функция синус (от аргумента, выраженного в радианах), а знак «!» обозначает факториальную функцию, упоминавшуюся уже в главе 8.iii. В математике, изучаемой в старших классах, вы встречались только с факториальной функцией, аргументами которой являются положительные целые числа: 2! = 1×2, 3! = 1×2×3, 4! = 1×2×3×4 и т.д. В высшей математике, однако, есть способ определить факториальную функцию для всех чисел, кроме отрицательных целых, для чего применяется прием расширения области определения вполне в духе того, которым мы только что пользовались. Например, (¹/₂)! оказывается равным 0,8862269254… (на самом деле — половине квадратного корня из π), (−¹/₄)! = 1,2254167024… и т.д. Отрицательные целые создают проблемы в этой формуле, но это не критические проблемы, и я ничего о них говорить не буду. На рисунке 9.11 изображена полная факториальная функция для аргументов от −4 до 4.