Читать книгу - "Путеводитель для влюблённых в математику - Эдвард Шейнерман"

Положительное целое число называется простым, если у него есть ровно два делителя: 1 и оно само.

Например, 17 – простое число, потому что 1 и 17 – его единственные делители. По той же причине 2 – простое число.

С другой стороны, 18 не является простым числом, потому что помимо 1 и самого себя оно делится на 2, 3, 6 и 9. Такие числа, как 18, называют составными. Если говорить математическим языком, то положительное целое число называют составным, если у него есть другие делители помимо 1 и самого себя.

Размежевание чисел на простые и составные касается всех натуральных чисел, кроме 1. Мы выделяем 1 в отдельную категорию и называем единичным элементом, или единицей^[15]. Кого-то расстраивает тот факт, что Плутон больше не причисляют к планетам, другие раздражены тем, что 1 не считается простым числом.

Если подытожить, у нас есть три категории положительных целых чисел:

• единица с одним положительным делителем;

• простое число с двумя положительными делителями;

• составное число с тремя и более положительными делителями.

Отмечу, что 1 – единственное в своем роде число, а вот составных чисел бесконечно много: 4, 6, 8, 10, 12 и т. д. – составные числа (и таких еще много).

Но сколько же простых чисел существует?

Разложение на множители

Разложить число на множители означает представить его в виде произведения. Рассмотрим число 84. Мы можем разложить его на множители несколькими способами, например:

2 × 42; 3 × 28; 12 × 7; 2 × 6 × 7; 21 × 4.

В пределе разложить на множители означает найти произведение простых чисел, например: 84 = 2 × 2 × 3 × 7. Нельзя разбить эти множители на части, потому что каждый из них представляет собой простое число. Разумеется, мы можем добавить какое-то количество единиц, например:

84 = 1 × 1 × 2 × 2 × 3 × 7,

но дополнительные множители усложняют, а не упрощают выражение, другие множители от этого не становятся меньше^[16].

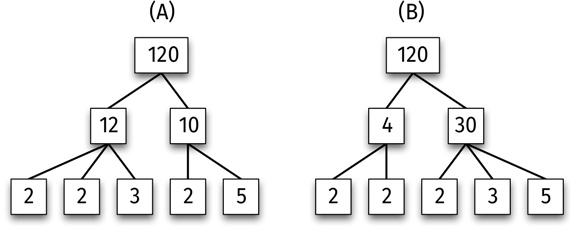
Возьмем другой пример: 120. Мы можем представить 120 как 12 × 10 и затем 12 как 2 × 2 × 3, а 10 – как 2 × 5. Это дает:

120 = (2 × 2 × 3) × (2 × 5). (A)

С другой стороны, мы можем начать так: 120 = 4 × 30 и далее заметить, что 4 = 2 × 2, а 30 = 2 × 3 × 5. Вместе это дает:

120 = (2 × 2) × (2 × 3 × 5). (B)

Важно отметить, что простые числа в выражениях (A) и (B) одинаковые, различается лишь порядок, в котором они перемножаются. Это показано на рисунке.

Любой способ представления числа 120 в качестве произведения простых чисел дает один и тот же результат.

Эта единственность разложения на множители зафиксирована в следующей теореме^[17].

Теорема (основная теорема арифметики). Любое положительное целое (натуральное) число может быть разложено на простые множители единственным образом (если пренебречь порядком множителей)^[18].

(Здесь необходимо небольшое пояснение. В случае, скажем, числа 30 это утверждение достаточно ясно. Мы можем представить 30 как 2 × 3 × 5 или как 5 × 3 × 2 – разницы нет, отличается лишь порядок множителей. Простое число имеет всего один простой множитель – само себя. Например, множитель 13 – это 13. Но как быть с 1? Принято говорить, что пустое произведение^[19] равно единичному элементу; таким образом, произведение отсутствующих элементов равно 1.)

Сочетая простые числа, мы выстраиваем все положительные целые числа. Простые числа – это атомы умножения.

Насколько много?

Вернемся к вопросу: сколько всего простых чисел существует? Ответ – на следующей строчке.

Теорема. Простых чисел бесконечно много.

Утверждение приписывают Евклиду^[20]. Доказательство этой теоремы – математическая жемчужина. Мы не можем доказать ее методом перебора. Очевидно, что время от времени в числовом ряде попадаются простые числа. Вот несколько первых простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 и 67.

Но чем дальше мы идем по последовательности простых чисел, тем обширнее становятся промежутки между ними. Если посмотреть на перечень выше, можно увидеть, что два числа отстоят друг от друга максимум на 6 единиц (например, 53 и 59). Но простые числа 89 и 97 отстоят друг от друга на 8 единиц, все целые числа между ними составные. Или вот другой пример: 139 и 149 – их отделяет 10 единиц. Чем дальше мы двигаемся, тем быстрее увеличиваются промежутки между соседними простыми числами. Можно предположить, что в конечном итоге простые числа должны совсем исчезнуть. На самом деле, хотя они и встречаются все реже, их список в числовом ряду не имеет конца. Впрочем, прежде чем говорить об этом уверенно, мы должны привести доказательство.