Читать книгу - "Путеводитель для влюблённых в математику - Эдвард Шейнерман"
Открой для себя врата в удивительный мир Читать книги / Домашняя книг на сайте books-lib.com! Здесь, в самой лучшей библиотеке мира, ты найдешь сокровища слова и истории, которые творят чудеса. Возьми свой любимый гаджет (Смартфоны, Планшеты, Ноутбуки, Компьютеры, Электронные книги (e-book readers), Другие поддерживаемые устройства) и погрузись в магию чтения книги 'Путеводитель для влюблённых в математику - Эдвард Шейнерман' автора Эдвард Шейнерман прямо сейчас – дарим тебе возможность читать онлайн бесплатно и неограниченно!
402 0 04:43, 26-05-2019Аннотация к книге "Путеводитель для влюблённых в математику - Эдвард Шейнерман", которую можно читать онлайн бесплатно без регистрации
Легко заметить: 1,4 слишком мало для квадратного корня из двух, а 1,5 – слишком велико. Следовательно, √2 лежит между этими двумя величинами.
Продолжим в том же духе. Будем возводить в квадрат числа между 1,4 и 1,5, двигаясь с шагом 0,01. Мы обнаружим, что 1,41² = 1,9881, а 1,42² = 2,0164. Из этого можно сделать умозаключение, что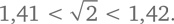
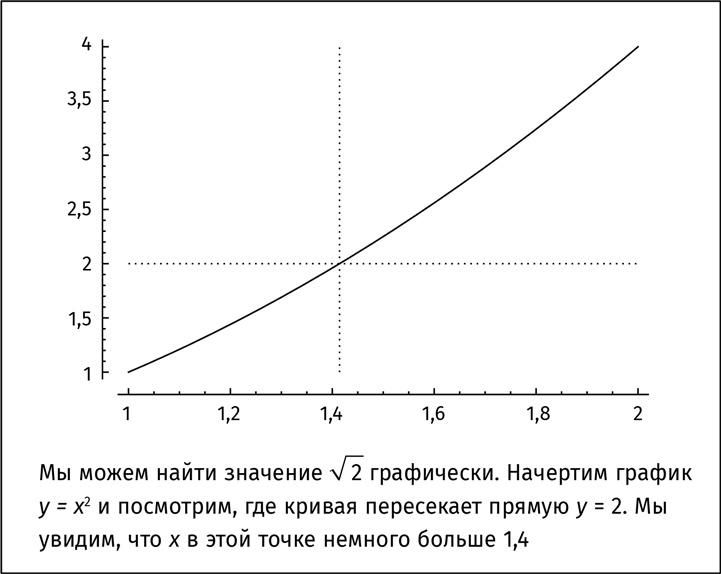
Мы можем двигаться таким образом все дальше и дальше, приближаясь к √2
Рано или поздно мы либо успокоимся (достигнув числа, фантастически близкого к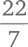
либо почувствуем отчаяние (увидев, что никогда не сможем точно вычислить √2
Но что означает это «точно»?
За границами рационального
Разумный способ определить точное значение числа – представить его в виде рационального числа, то есть отношения двух целых чисел. Если бы мы сумели представить √2 в виде дроби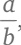
где a и b – целые числа, мы бы нашли его точное значение.
Увы, но такое невозможно. Однако это нужно доказать.
Теорема. √2 не является рациональным числом.
Будем идти от противного, как и в главе 1, где мы подсчитывали количество простых чисел. Предположим, что √2 – рациональное число. Если это допущение приведет к абсурдным выводам, значит, оно несостоятельно.
Итак, приступим. Если √2 – рациональное число, его можно выразить в виде отношения двух целых чисел:
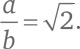
Возведем обе части тождества в квадрат:
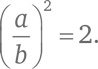
Раскроем скобки:
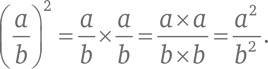
Таким образом:
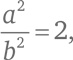
или:
2b² = a². (С)
Если a – целое число, мы можем разложить его на простые множители, причем (согласно основной теореме арифметики) одним-единственным способом:
a = p1 × p2 × … × pn.
Проделаем аналогичную процедуру с b:
b = q1 × q2 × … × qm.
Следовательно, левую часть равенства (С) можно представить в таком виде:
2b² = 2 × (q1 × q2 × … × qm)² = 2 × (q1 × q1) × (q2 × q2) × … × (qm × qm).
Несложно заметить, что 2b² раскладывается на нечетное число простых множителей.
Аналогично поступаем с правой частью (С):
a² = (p1 × p2 × … × pn) ² = (p1 × p1) × (p2 × p2) × … × (pn × pn).
В отличие от 2b², выражение a² раскладывается на четное число простых множителей.
Подытожим. В соответствии с нашим предположением 2b² = a². Это означает, что некоторое число одновременно можно разложить на четное и нечетное количество простых множителей. Но это противоречит основной теореме арифметики.
Мы пришли к невозможному выводу. Таким образом, наша изначальная посылка была ошибочна. Следовательно, √2 не является рациональным числом.
Такие числа, как √2 называют иррациональными. Рациональные числа хороши для операций с физическими величинами[43], но их недостаточно для всех математических величин. Длина диагонали квадрата 1 × 1 – иррациональное число.
Конструктивные числа
Начав с числа 1 и шаг за шагом проделывая операции сложения, вычитания и умножения, мы можем получить любое целое число, но и только. Если мы добавим операцию деления, нам откроются все рациональные числа, но ими же мы и будем ограничены.
Если мы введем операцию извлечения квадратного корня[44], то получим числа, которые не являются отношением целых чисел. Например:
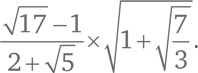
Для удобства мы будем называть конструктивными такие числа, которые можно получить с помощью числа 1 и пяти операций – сложения, вычитания, умножения, деления и извлечения квадратного корня – с привычными оговорками: нельзя делить на ноль и извлекать корень из отрицательных величин.
Разумеется, возникает вопрос: все ли числа конструктивные?
Древние греки усматривали магическую внутреннюю связь между арифметикой и геометрией. Эта связь подтверждалась операциями с использованием двух инструментов: линейки без делений и циркуля. Возьмем отрезок единичной длины; какова может быть длина отрезков, построенных на его основе с помощью карандаша, линейки без делений и циркуля?
Конец ознакомительного фрагмента Купить полную версию книги
Прочитали книгу? Предлагаем вам поделится своим впечатлением! Ваш отзыв будет полезен читателям, которые еще только собираются познакомиться с произведением.
Оставить комментарий
-
Гость Елена12 июнь 19:12
Потрясающий роман , очень интересно. Обожаю Анну Джейн спасибо 💗
Поклонник - Анна Джейн
-
Гость24 май 20:12
Супер! Читайте, не пожалеете
Правила нежных предательств - Инга Максимовская
-
Гость Наталья21 май 03:36
Талантливо и интересно написано. И сюжет не банальный, и слог отличный. А самое главное -любовная линия без слащавости и тошнотного романтизма.
Вторая попытка леди Тейл 2 - Мстислава Черная
-
Гость Владимир23 март 20:08
Динамичный и захватывающий военный роман, который мастерски сочетает драматизм событий и напряжённые боевые сцены, погружая в атмосферу героизма и мужества.
Боевой сплав - Сергей Иванович Зверев