Читать книгу - "Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике - Джон Дербишир"

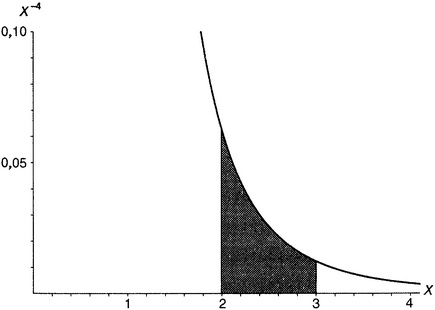
Рисунок 7.3. Для чего пригодно интегрирование.

Функция, показанная на рисунке 7.3, а это в действительности функция 1/x⁴, т.е., другими словами, x⁻⁴, — ограничивает собой некоторую площадь между аргументами x = 2 и x = 3. Чтобы найти эту площадь, сначала надо найти интеграл от x⁻⁴. Согласно приведенному выше общему правилу, этот интеграл равен −¹/₃x⁻³, т.е. −1/(3x³). Эта функция, как и всякая другая, имеет значение для каждого x из своей области определения. Чтобы найти площадь между аргументами 2 и 3, надо вычислить значение интеграла при аргументе 3, затем вычислить значение интеграла при аргументе 2, а потом вычесть второе значение из первого.

При x = 3 значение функции −1/(3x³) равно −¹/₈₁, при x = 2 оно составляет −¹/₂₄. Вычитаем, не забывая, что вычесть отрицательное число — это все равно что прибавить соответствующее положительное: −¹/₈₁ − (−¹/₂₄) = ¹/₂₄ − ¹/₈₁, что равно ¹⁹/₆₄₈, т.е. примерно 0,029321.

У математиков есть специальный способ для записи всей этой процедуры: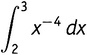, что читается как «интеграл от икс в минус четвертой степени по дэ-икс от двух до трех». (Не слишком озадачивайтесь этим самым «по dх» — назначение этих слов состоит в указании, что именно x является основной переменной, с которой мы работаем, и именно ее интеграл надо найти. Если под знаком интеграла окажутся еще другие переменные, то они будут там присутствовать праздно, интегрирование ведется не по ним. В главе 19 у нас появится такой пример.)

Далее. Иногда оказывается возможным отправить правый конец интегрирования на бесконечность, но при этом получить конечную площадь. Это напоминает ситуацию с бесконечными суммами: если значения ведут себя должным образом, такие суммы могут сходиться к конечному значению. То же и здесь. У функций, которые ведут себя должным образом, площадь под кривой может оказаться конечной, несмотря даже на то, что область бесконечно длинная. Интегралы связаны с суммами на глубинном уровне. Даже знак интеграла, впервые использованный Лейбницем в 1675 году, представляет собой вытянутое S, обозначающее «сумму».

Смотрите: предположим, что вместо того, чтобы останавливаться на тройке, мы бы продолжили интегрирование до x = 100. Тогда, поскольку куб числа 100 равен 1 000 000, наше вычисление приобрело бы вид:

(−¹/_{3 000 000}) − (−¹/₂₄) = ¹/₂₄ − ¹/_{3 000 000}.

Ясно, что если бы мы пошли еще дальше, то второе слагаемое стало бы еще меньше. По мере того как мы спешим к бесконечности, оно постепенно угасает, стремясь к нулю, и у нас есть полное право написать:

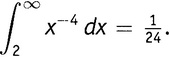
Стоит заметить, что, когда интеграл используется для вычисления площади, x исчезает из ответа: вместо x подставляются числа и в ответе получается число.

Вот и все. Клянусь, это все, что нам понадобится из дифференциального и интегрального исчисления. И поскольку ничего нового вводиться не будет, пользоваться дифференциальным и интегральным исчислением мы начнем прямо сейчас. С их помощью мы определим новую функцию, которая чрезвычайно важна в теории простых чисел и дзета-функции.

VIII.

Сначала рассмотрим функцию 1/ln t. Ее график показан на рисунке 7.4. Обозначение для аргумента заменено с x на t по той причине, что букве x отведена другая роль, чем просто быть бессловесной переменной.

На рисунке затемнена некоторая область под графиком, поскольку мы сейчас устроим небольшое интегрирование. Как только что объяснялось, интегрирование — это способ вычислить площадь под графиком функции. Сначала надо найти интеграл от интересующей нас функции, а потом взять калькулятор. Итак, каков же интеграл от функции 1/ln t?

К сожалению, в домашнем хозяйстве нет обычной функции, которая позволила бы выразить интеграл от 1/ln t. Но интеграл этот весьма важен. Он снова и снова появляется в исследованиях, связанных с Гипотезой Римана. Поскольку нежелательно писать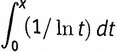 всякий раз, как потребуется эта монструозная конструкция, мы попросту определим новую функцию, выражаемую этим интегралом, и выдадим ей свидетельство, что это добропорядочная и уважаемая функция, ни в чем не уступающая другим своим коллегам.

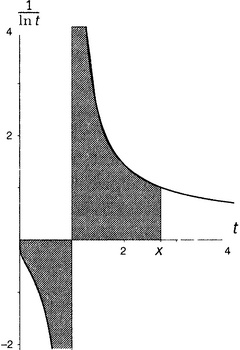
Рисунок 7.4. Функция 1/ln t.

У этой новой функции есть имя: ее зовут интегральный логарифм. Для нее обычно используется обозначение Li(x). (Иногда пишут li(х).) Она определена как функция, выражающая площадь под кривой — то есть под графиком функции 1/ln t — от нуля до x.^[59]