Читать книгу - "Как не ошибаться. Сила математического мышления - Джордан Элленберг"
Аннотация к книге "Как не ошибаться. Сила математического мышления - Джордан Элленберг", которую можно читать онлайн бесплатно без регистрации
Однако статья в журнале Obesity скрывает еще худшее преступление против математики и здравого смысла. Сделать линейную регрессию довольно легко – и как только вы выполнили ее один раз, возникает соблазн делать это и дальше. Поэтому Ванг и его коллеги разбили свои данные на категории по этнической и половой принадлежности. Например, оказалось, что чернокожие мужчины с меньшей вероятностью имеют избыточный вес, чем американцы в целом. Еще важнее, что среди чернокожих мужчин количество людей с избыточным весом увеличивалось в два раза медленнее. Если мы отобразим на одном рисунке графики увеличения доли людей с избыточным весом среди чернокожих мужчин и среди всех американцев, а также линейную регрессию, построенную Вангом и его коллегами, получится следующая картина.
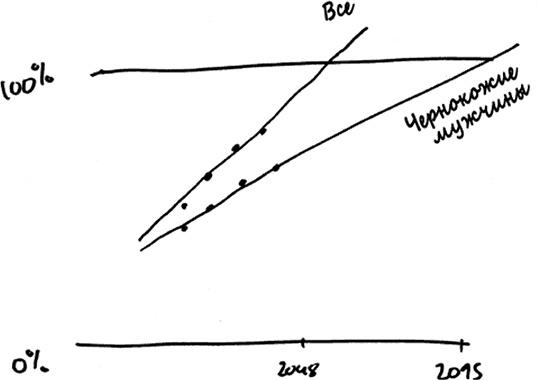
Молодцы, чернокожие! Вы не будете жирными вплоть до 2095 года, а в 2048 году ожирение распространится лишь у 80 %.
Видите, в чем проблема? Если предполагается, что в 2048 году все американцы будут иметь избыточный вес, где же будут те чернокожие мужчины, у которых не возникнет в будущем никаких проблем с весом? За пределами страны?
В статье это противоречие осталось без внимания. А ведь это эпидемиологический эквивалент утверждения о −4 граммах воды в кувшине. Ноль зачетных баллов.
Сколько это в мертвых американцах?
Насколько серьезен конфликт на Ближнем Востоке? Эксперт по вопросам борьбы с терроризмом Дэниел Баймен из Джорджтаунского университета приводит в Foreign Affairs холодные, безжалостные цифры: «Израильские военные сообщают о том, что с начала второй интифады [2000 год. – Д. Э.] до конца октября 2005 года палестинцы убили 1074 и ранили 7520 израильтян – для такой маленькой страны поразительные данные, пропорциональный эквивалент которых составляет 50 тысяч убитых и 300 тысяч раненых американцев»{33}. Такие подсчеты часто используются во время обсуждения ситуации в ближневосточном регионе. В декабре 2001 года Палата представителей Конгресса США заявила о том, что гибель 26 человек во время серии атак в Израиле «пропорционально смерти 1200 американцев»{34}. Ньют Гингрич писал в 2006 году{35}: «Помните о том, что, когда Израиль теряет восемь человек, с учетом разницы в численности населения это эквивалентно потере почти 500 американцев»{36}. Не желая уступать авторам этих высказываний, Ахмед Мур написал в Los Angeles Times следующее: «Когда во время операции “Литой свинец” в секторе Газа Израиль убил 1400 палестинцев – что пропорционально 300 тысячам американцев, – будущий президент Обама хранил молчание»{37}.
Риторика с использованием пропорций не является исключительным правом, закрепленным лишь за Святой землей. Джеральд Каплан писал в 1988 году: «За последние восемь лет погибли, ранены или похищены с обеих сторон противостояния около 45 тысяч никарагуанцев – это эквивалентно 300 тысячам канадцев или 3 миллионам американцев»{38}. Министр обороны США в период Вьетнамской войны Роберт Макнамара сказал в 1997 году, что почти 4 миллиона погибших во время войны вьетнамцев «эквивалентны 27 миллионам американцев»{39}. Каждый раз, когда в какой-либо небольшой стране погибает много людей, авторы редакционных статей достают свои логарифмические линейки и начинают подсчитывать: сколько этих погибших «укладывается» в мертвых американцах?
Вот как можно получить эти цифры. Погибшие от рук террористов 1074 израильтян составляют 0,015 % от общей численности населения Израиля (которая в период с 2000 по 2005 год составляла от 6 до 7 миллионов). Далее все эти эксперты приходят к выводу, что смерть 0,015 % американского населения (что составляет около 50 тысяч человек) имела бы в данном случае такой же эффект.
Это линеоцентризм в чистейшей форме. Согласно аргументации с использованием пропорций, эквивалент 1074 израильтян в любой точке земного шара можно найти с помощью такого графика.
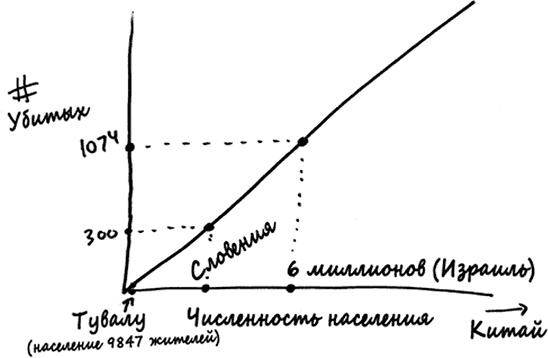
Количество израильских жертв – 1074 человек – эквивалентно 7700 испанцев или 223 тысяч китайцев, но всего 300 словенцев и одному или двум тувалуанцам.
Со временем (а может быть, и с самого начала?) такая аргументация начинает рушиться. Когда в момент закрытия в баре остается два человека и один из них сбивает с ног другого, это совсем не эквивалентно тому, что в это же время удар получают 150 миллионов американцев.
Еще один пример. Все согласны с тем, что одно из самых страшных преступлений столетия – когда в 1994 году было уничтожено 11 % населения Руанды. Но мы не рассуждаем об этом кровопролитии так: «С точки зрения Европы сороковых это было в девять раз хуже холокоста». Малейшая попытка сделать это вызвала бы настоящее отвращение.
Вот одно из важнейших правил математической гигиены: когда вы проверяете на практике тот или иной математический метод, попробуйте выполнить одни и те же расчеты несколькими разными способами. Если получите в результате разные ответы, значит, с вашим методом что-то не так.
Возьмем такой пример. На железнодорожном вокзале Аточа в результате взрыва бомбы в 2004 году погибло 200 человек[63]. Каким был бы эквивалентный итог взрыва бомбы на Центральном железнодорожном вокзале в Нью-Йорке?
Численность населения Соединенных Штатов Америки в семь раз превышает численность населения Испании. Следовательно, если представить 200 человек как 0,0004 % от населения Испании, эквивалентный террористический акт в США привел бы к гибели 1300 человек. С другой стороны, 200 человек составляют 0,006 % от населения Мадрида; пропорциональное увеличение этого количества с учетом численности населения Нью-Йорка, которая в два с половиной раза больше населения Мадрида, дает 463 жертвы. Или нам следует сопоставить провинцию Мадрид со штатом Нью-Йорк? В таком случае мы получили бы цифру около 600 жертв. Такую неоднозначность результатов необходимо расценивать как тревожный сигнал: метод пропорций не внушает доверия.
Прочитали книгу? Предлагаем вам поделится своим впечатлением! Ваш отзыв будет полезен читателям, которые еще только собираются познакомиться с произведением.
Оставить комментарий
-
 Илья12 январь 15:30
Книга прекрасная особенно потому что Ее дали в полном виде а не в отрывке
Горький пепел - Ирина Котова
Илья12 январь 15:30
Книга прекрасная особенно потому что Ее дали в полном виде а не в отрывке
Горький пепел - Ирина Котова
-
 Гость Алексей04 январь 19:45
По фрагменту нечего комментировать.
Бригадный генерал. Плацдарм для одиночки - Макс Глебов
Гость Алексей04 январь 19:45
По фрагменту нечего комментировать.
Бригадный генерал. Плацдарм для одиночки - Макс Глебов
-
 Гость галина01 январь 18:22
Очень интересная книга. Читаю с удовольствием, не отрываясь. Спасибо! А где продолжение? Интересно же знать, а что дальше?
Чужой мир 3. Игры с хищниками - Альбер Торш
Гость галина01 январь 18:22
Очень интересная книга. Читаю с удовольствием, не отрываясь. Спасибо! А где продолжение? Интересно же знать, а что дальше?
Чужой мир 3. Игры с хищниками - Альбер Торш
-
 Олена кам22 декабрь 06:54
Слушаю по порядку эту серию книг про Дашу Васильеву. Мне очень нравится. Но вот уже третий день захожу, нажимаю на треугольник и ничего не происходит. Не включается
Донцова Дарья - Дантисты тоже плачут
Олена кам22 декабрь 06:54
Слушаю по порядку эту серию книг про Дашу Васильеву. Мне очень нравится. Но вот уже третий день захожу, нажимаю на треугольник и ничего не происходит. Не включается
Донцова Дарья - Дантисты тоже плачут





