Читать книгу - "Алекс в стране чисел. Необычайное путешествие в волшебный мир математики - Алекс Беллос"

Игроки в «Мега-Миллионс» должны выбрать пять чисел от 1 до 56 и одно от 1 до 46. Имеется около 175 миллионов возможных комбинаций. Как перечислить все эти комбинации таким образом, чтобы каждая из них встречалась только один раз, без дублирования? В начале 1960-х годов румынский математик Стефан Мандел задался этим вопросом относительно румынской лотереи, которая по масштабу гораздо меньше американских. Получить ответ оказалось совсем непросто. Мандел, однако, в конце концов решил задачу, правда потратив на нее несколько лет, и стал победителем в румынской лотерее 1964 года. (Он не скупил все комбинации, потому что это было бы слишком дорого, а применил вспомогательный метод, называемый «уплотнением», который гарантирует, что по крайней мере 5 из 6 чисел будут правильными. Обычно за угадывание 5 чисел полагается второй приз, но ему повезло, и он сразу же выиграл главный.) Записанный на бумаге алгоритм Мандела, позволяющий определить те комбинации, которые надо покупать, занял 8000 страниц. Вскоре после получения выигрыша он эмигрировал в Израиль, а затем в Австралию.

Уже в Мельбурне Мандел основал международный синдикат по лотерейным ставкам, собрав с его участников достаточно денег для того, чтобы при желании иметь возможность скупить все комбинации в лотерее. Он следил за проводимыми по всему миру лотереями с переходящими джекпотами, как минимум в три раза превышающими суммарную цену покупки всех комбинаций. В 1992 году в поле его зрения попала лотерея штата Виргиния, в которой было семь миллионов комбинаций, а каждый билет стоил 1 доллар, при том что джекпот достиг почти 28 миллионов долларов. Тогда Мандел принялся за дело. Он печатал купоны в Австралии, заполнял их на компьютере так, чтобы они охватили все семь миллионов комбинаций, а затем отправлял самолетом в Соединенные Штаты. И — получил главный приз, а заодно и 135 000 вторых призов!

Лотерея в Виргинии была самым большим из сорванных Манделом джекпотов, доведя счет его побед, одержанных после отъезда из Румынии, до 13. Служба внутренних доходов США (The U.S. Internal Revenue Service), ФБР, и ЦРУ проявили интерес к синдикату Мандела и попытались расследовать его методы участия в лотерее, но ничего противоправного эти уважаемые организации не нашли. Ведь нет ничего незаконного в том, чтобы скупить все комбинации, хотя это и слегка отдает аферой. Мандел в настоящее время отошел от дел, связанных с лотереями, и наслаждается жизнью на одном из тропических островов южной части Тихого океана^[59].

* * *

Особенно выразительное и наглядное представление случайности изобрел в 1888 году Джон Венн (1834–1923). Венн, быть может, — наименее яркий из всех математиков, имя которых постоянно на слуху. Он был кембриджским профессором и англиканским клириком и провел большую часть жизни, занимаясь составлением сборника биографий 136 000 выпускников Кембриджа, получивших дипломы до 1900 года. Никаких революционных прорывов в своей науке он не совершил, но тем не менее разработал замечательный способ для объяснения логических рассуждений с помощью пересекающихся окружностей. Хотя в предшествующие столетия и Лейбниц, и Эйлер рассматривали нечто очень похожее, диаграммы были названы в честь Венна^[60]. Гораздо меньше известно, что Венн придумал блестящий способ для иллюстрации случайности.

Представим себе точку, поставленную в центре белого листа бумаги. Из этой точки выходят восемь возможных направлений: на север, северо-восток, восток, юго-восток, юг, юго-запад, запад и северо-запад. Припишем этим направлениям числа от 0 до 7. Случайным образом выберем число от 0 до 7 и проведем отрезок прямой в направлении, отвечающем полученному числу. Будем делать так снова и снова, в результате чего на бумаге появится некая кривая. Венн проделал такое для самой непредсказуемой из известных ему числовых последовательностей — десятичного разложения числа π (откуда исключил восьмерки и девятки)^[61]. Результат, писал он, представлял собой «очень правильное наглядное представление случайности».

Построенный Венном чертеж стал, по-видимому, самой первой диаграммой «случайного блуждания». То же самое нередко называют «блужданием пьяницы», апеллируя к более выразительной картинке, на которой вместо исходной точки — фонарный столб, а вместо числа π — человек в состоянии сильного опьянения, совершающий неуверенные движения. Один из самых очевидных вопросов, которые здесь напрашиваются, — насколько далеко пьяница сумеет отойти от столба, пока еще стоит на ногах? В среднем, чем дольше он будет блуждать, тем дальше от столба окажется. Выяснилось, что расстояние между пьяницей и фонарем растет как квадратный корень из времени прогулки. Итак, если за один час наш пьянчужка в среднем проходит один квартал, то, если дать ему четыре часа, он пройдет два квартала, а через девять часов — три.

Во время своего случайного блуждания наш подвыпивший герой будет иногда ходить кругами, повторяя собственные шаги. Какова вероятность, что он в конце концов снова набредет на фонарный столб? Как ни странно, ответ таков: 100 процентов! Он может блуждать годами в самых отдаленных уголках, но будьте уверены — если дать ему достаточно времени, он в конце концов обязательно вернется в исходную точку.

Представим себе, что пьяница блуждает в трех измерениях. Назовем это «полетом одурелого шмеля». Шмель стартует из некоторой точки в трехмерном пространстве и летит в случайном направлении на фиксированное расстояние по прямой. Затем он останавливается, переводит дух и снова, жужжа, срывается с места в другом случайном направлении, пролетая то же самое расстояние. И так далее. Какова вероятность, что в конце концов он вернется в точку своего старта? Ответ: всего 0,34, то есть около трети. Не правда ли, довольно странно, что в двух измерениях возвращение пьяницы к фонарному столбу представляло собой абсолютную определенность, но еще более странно то, что шмель, жужжащий в воздухе неограниченно долго, с высокой вероятностью никогда не вернется домой.

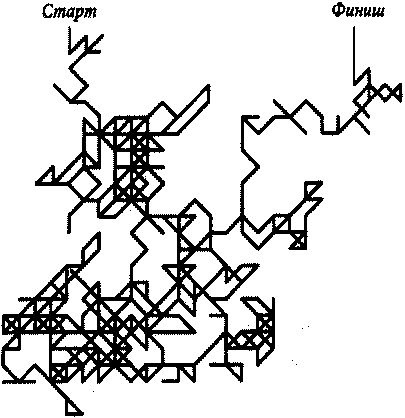
Первый в мире пример случайного блуждания. Из книги Джона Венна «Логика шанса» (1866). Траектория задается цифрами из разложения числа π, начиная с 1415

Главный герой романа-бестселлера Люка Рейнхарта «Дайсмен» («Человек — Игральная кость») принимает жизненно важные решения, бросая игральную кость. Представим себе «Человека-монету», который принимает решения, подбрасывая монету. Если, скажем, у него выпадает орел, он передвигается на один шаг вверх по странице, а если решка — то вниз. Путь нашего Человека-монеты подобен блужданиям уже знакомого нам пьяницы, но в одном измерении, ведь он может смещаться только вдоль одной и той же прямой. Изобразим на графике случайные блуждания, описываемые вторым из двух отчетов о 30 бросаниях монеты, приведенных ранее. Получается вот что: