Читать книгу - "Большой роман о математике. История мира через призму математики - Микаэль Лонэ"

С появлением чисел математика практически сразу разделилась на несколько направлений. Арифметика, логика, алгебра постепенно становились самостоятельными дисциплинами.

Одной из наиболее стремительно развивающихся дисциплин в эпоху Античности была геометрия. Она оставила в веках таких великих мыслителей прошлого как Фалес, Пифагор или Архимед, имена которых и по сей день мы встречаем на страницах школьных учебников.

Однако еще до того момента, когда геометрия стала самостоятельной дисциплиной, сама земля была ее непосредственным предметом анализа. Этимология слова подсказывает нам, что первоочередной задачей геометрии являлось измерение земли, что, таким образом, отчасти делает землемеров первыми геометрами. Задача разделения земельных участков всегда была одной из самых важных. Как разделить поле на равные части? Как рассчитать стоимость земельного участка исходя из его площади? Какая из этих двух частей находится ближе к реке? Как должен быть проложен канал, чтобы маршрут по нему оказался наиболее коротким?

Все эти вопросы были крайне важны для цивилизаций Античности, экономика которых строилась вокруг сельского хозяйства и, таким образом, на разделении земельных участков. Для того чтобы ответить на эти вопросы, знания из области геометрии развивались, обогащались и передавались из поколения в поколение, а умение ими оперировать, без сомнения, являлось одним из центральных аспектов жизни общества.

Для древних специалистов по измерению земель веревка была подчас первым геометрическим инструментом. В Древнем Египте существовала даже отдельная профессия – натягиватель веревки. Поскольку Нил регулярно выходил из берегов, именно люди этой профессии сообщали об изменении границ реки. Они вбивали столбики вдоль реки и натягивали веревки по границам полей в тех местах, где, согласно их вычислениям, должен был находиться край вышедшего из берегов Нила.

Возводя здание, также в первую очередь натягивали веревки на земле, точно обозначая границы будущего строения согласно плану архитектора. При строительстве дворца или иного значительного сооружения первую веревку зачастую натягивал в качестве символического жеста лично фараон.

Необходимо отметить, что веревка могла выполнять роль сразу нескольких геометрических инструментов. Землемеры использовали веревку как линейку, циркуль и треугольник с прямым углом.

Использовать веревку как линейку очень просто: ее достаточно натянуть между двумя зафиксированными точками, и получалась идеально ровная линия. Если требовалось определить длину, достаточно было сделать узлы на одинаковых расстояниях друг от друга по длине веревки. Использовать ее в качестве циркуля также было совсем не сложно. Одна из точек фиксировалась в земле, а точкой на веревке очерчивалась окружность на земле – так получался ровный круг. Чтобы начертить окружность определенного радиуса, достаточно было сделать разметку на веревке и начертить окружность, используя точку на веревке, расположенную на соответствующем количестве размеченных отрезков от центра.

А вот для того, чтобы использовать веревку для разметки угла, наоборот, требовалось приложить определенные усилия. Давайте на минуточку задумаемся над конкретной задачей: как изобразить прямой угол? На ум сразу приходят несколько способов. Если, например, нарисовать две окружности, пересекающиеся между собой, а затем соединить их центры и две точки пересечения, то две полученные линии будут перпендикулярны друг другу, образуя, таким образом, прямой угол.

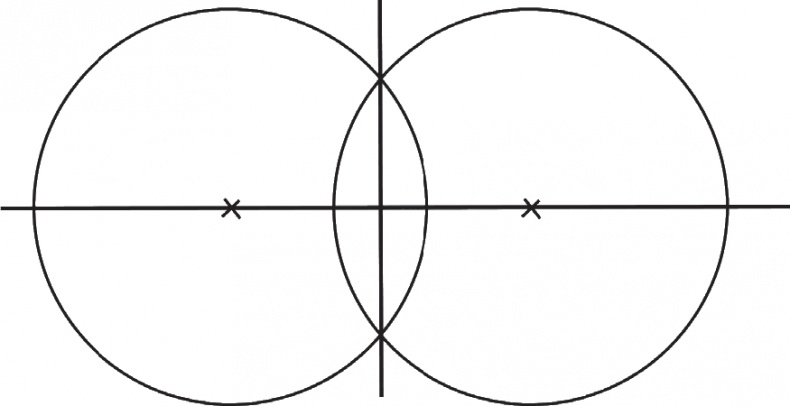
С теоретической точки зрения этот способ безупречен, но вот на практике пользоваться им крайне неудобно. Представьте, как землемеры выходят на поле и начинают расчерчивать две окружности каждый раз, когда им требуется разметить прямой угол или проверить точность уже размеченных перпендикулярных линий. Такой способ оказывается на деле небыстрым и неэффективным.

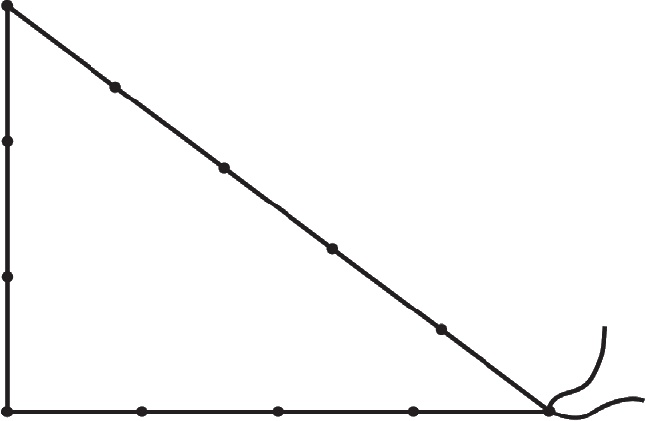
Однако был и более практичный метод, который активно использовали землемеры: образование треугольника с прямым углом, используя саму веревку. Такой треугольник получил название прямоугольный треугольник. И самый распространенный среди них – со сторонами 3–4–5! Если вы возьмете веревку, разделенную на двенадцать частей тринадцатью узлами, вы сможете образовать треугольник со сторонами в 3, 4 и 5 интервалов соответственно. И магическим образом угол, образованный сторонами в 3 и 4 интервала, будет прямым.

За 4000 лет до этого жители Вавилона уже разработали специальные таблицы, позволяющие делать прямоугольные треугольники. Табличка «Плимптон 322», которая в настоящее время хранится в коллекции Колумбийского университета в Нью-Йорке, была создана приблизительно в 1800 г. до н. э. и представляет собой таблицу из пятнадцати комбинаций таких чисел. Помимо 3–4–5 там приводятся еще четырнадцать комбинаций, среди которых такие сложные, как 65–72–97 и даже 1679–2400–2929. За исключением нескольких незначительных опечаток, ставших следствием ошибки в расчетах или неправильного переписывания, треугольники из Плимптонской таблицы абсолютно правильные: в каждом из них есть прямой угол!

Сложно точно сказать, с какого момента вавилонские землемеры начали использовать свои познания об определении прямого угла на земле. В любом случае эти знания нашли свое применение много лет спустя исчезновения шумерской цивилизации. В Средние века веревка с тринадцатью узлами, также известная как веревка друидов, повсеместно использовалась при строительстве соборов.

Путешествуя по истории математики, часто отмечают, что ряд похожих выводов был сделан одновременно и независимо друг от друга в разных концах нашей планеты учеными, жившими за тысячи километров друг от друга в совершенно разных обществах. Удивительно странным совпадением является то, что в китайской цивилизации I в. до н. э. были сделаны открытия в области математики, очень схожие с аналогичными открытиями этого времени цивилизаций Древнего Вавилона, Египта и Греции.