Читать книгу - "Искушение астрологией, или Предсказание как искусство - Дэвид Берлински"

Иоганн Кеплер никогда не чувствовал себя в Праге как дома. Было что-то такое в задумчивой аристократической красоте этого города, что не соответствовало его темпераменту. Его жена, Барбара Мюллер, дважды ставшая вдовой до того, как вышла замуж за Кеплера, томилась в чешской столице еще больше, чем он. Она все время была недовольна. Ей не нравились погода, смена времен года, язык и еда. Тем не менее Прага стала для них убежищем. И Кеплер воображал, что заключит перемирие с темными улицами города и снег будет сыпаться на колокольни, словно мука через сито, или бесшумно опускаться во Влтаву, а ночной сторож в капюшоне — помахивать фонарем в арке и выкрикивать по-чешски: «Который час?» Здесь Кеплера ждала работа. В конце концов, он был императорским математиком.

Но вскоре на него обрушились несчастья. В Центральной Европе разгорался костер Тридцатилетней войны^[38]. Каждая воюющая сторона намеревалась выпустить свои коготки в глупой надежде, что другие их испугаются. В Прагу вошли солдаты. Их огромные громыхающие ботинки оставляли грязь в изысканных средневековых двориках. Город стал не только местом встреч для дипломатов и опытных жуликов, но и пристанищем вредоносных микробов, переносимых по Европе солдатами. Жена Кеплера тяжело заболела и тихо кашляла по ночам. Его покровитель Рудольф II был вынужден отречься от престола в пользу своего сводного брата. Целыми днями бывший император сидел в своих покоях, отказываясь принимать гостей и дипломатов. Он был правителем неавторитетным, но и не злобным. Теперь его отстранили от власти.

Жить и дальше в Праге Кеплер уже не мог. Вечерним ужинам и ночам, которые он проводил, дрожа, в своих неотапливаемых комнатах, богемскому пиву и роскошным пирам, от которых его нежный желудок завязывался в узел, долгим прогулкам в одиночестве по холодному лесу — всему пришел конец.

С трудом Кеплеру удалось найти работу математика в Линце. Перспектива вернуться в родную страну его радовала. Он хотел переехать туда хотя бы ради жены. Напуганная, больная, она мечтала о милых, таких родных звуках немецкого языка и привычном укладе жизни. Барбара Мюллер умерла в июле 1611 года от сыпного тифа. В душе Кеплера поселился мрак.

С мужеством, тем более заслуживающим восхищения, что было проявлено оно при столь грустных обстоятельствах, Кеплер продолжал работать. Его величайший труд был еще впереди.

Harmonicum Mundi («Гармония мира») — шедевр Иоганна Кеплера. Книга масштабна по охвату тем и богата математическими открытиями. Это величайший в истории труд по астрологии, хотя бы потому, что он единственный в этой сфере, написанный гением [150].

Цели Кеплера здесь неотделимы от его средств, а средства его — геометрические. В Mysterium Cosmographicum он расслышал мелодию, звучавшую в космосе. И объяснил одну ее часть, обратившись к пяти Платоновым телам. В Harmonicum Mundi эта мелодия становится контрапунктом.

Во Вселенной существуют две формы гармонии, утверждал Кеплер, — музыкальная и пространственная. Музыкальные гармонии передаются с помощью деления прямой линии на пропорциональные отрезки, пространственные — с помощью деления круга на сегменты. Музыкальные гармонии порождают созвучия, пространственные — аспекты, и в особенности астрологические аспекты.

Кеплер-математик принимает эстафету у другого Кеплера, ворчливого и придирчивого, — физика, скорбящего мужа, просителя, астронома, мистика и астролога. Кеплер принимает прямую и круг как основы, фигуры, существующие в самой природе, а стало быть, имманентные человеческой душе.

Приведем несколько необходимых определений, дабы проследить за работой проницательного Кеплерова ума. Многоугольник — простая фигура с определенным количеством сторон. Например, у треугольника их три, у квадрата четыре, у пятиугольника пять и так далее до фигур с тысячами сторон. Правильный многоугольник — тот, у которого все стороны равны. Равносторонний треугольник — да, подходит, а равнобедренный — нет. Квадрат — да, прямоугольник — нет.

Некоторые правильные многоугольники, замечает Кеплер, можно построить с помощью линейки и циркуля, классических инструментов евклидовой геометрии. Такие многоугольники познаваемы, все прочие непознаваемые. Познаваемые многоугольники, считал Кеплер, — это опорные точки миропорядка, положенные на плоскость Богом.

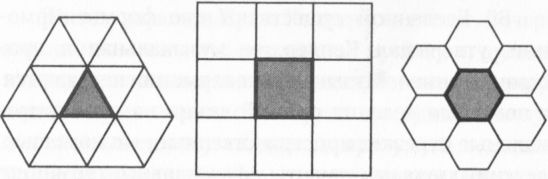
Мозаика на плоскости из треугольников, квадратов и шестиугольников

Если многоугольники можно классифицировать на основании того, что они собой представляют, рассуждает далее Кеплер, то тогда и на основании того, что они делают. Геометрическая плоскость сама по себе начисто лишена какой-либо структуры. У нее есть два измерения, но никаких внутренних особенностей. Однако, взяв бесконечное количество квадратов, математик может покрыть плоскость ими, ставя их подряд, так, чтобы не оставалось зазоров. В результате получится мозаика плоскости. А пятиугольник, напротив, не может закрыть плоскость мозаикой. И не важно, каким образом располагаются эти пять сторон, в любом случае где-то плоскость будет проглядывать.

Кеплер открыл три удивительных звездных многогранника. На рисунке изображен самый простой из них. Весь многогранник можно выложить мозаикой из правильных плоских фигур — в данном случае треугольников

Именно это обстоятельство подсказало Кеплеру вторую схему для классификации — и второй способ классификации правильных многоугольников. Те многоугольники, которые можно сложить так, чтобы получилась мозаика, Кеплер назвал контактными, а остальные неконтактными. Всего три правильных многоугольника контактны сами с собой, иначе говоря, самоконтактны, если построить такой неологизм. Это равносторонний треугольник, квадрат и шестиугольник.

Но по тому же признаку разные виды самоконтактных многоугольников могут объединяться друг с другом и складываться в собственную мозаику: квадраты с треугольниками или шестиугольники с квадратами. Получится полуправильная мозаика на плоскости.

Переходим на следующий, последний уровень сложности. Сложить мозаику можно не только на плоскости. Платоновы тела заполняют часть пространства и, таким образом, существуют в трех измерениях. Но каждое тело составлено из граней, которые сами по себе — правильные многоугольники. Вот что такое куб, если не шесть блуждающих квадратов, встретившихся в восьми ожидавших их вершинах? Тела, образованные таким способом, называются однородными многогранниками, они покрываются правильными прямоугольниками со стороны соответствующих им многоугольников по принципу квадрат к кубу. Но мозаичные многогранники выходят за пределы тел Платона лишь немного, включая в себя три эффектных звездных многогранника, открытых Кеплером. И это опять трехмерные тела, чьи грани могут быть покрыты набором правильных многоугольников.