Читать книгу - "Математика для любознательных (сборник) - Яков Перельман"

В следующих витринах галлереи нас поражают числовые достопримечательности совсем особого рода - некоторое подобие пирамид, составленных из чисел. Рассмотрим поближе первую из таких «пирамид».

Задача № 34

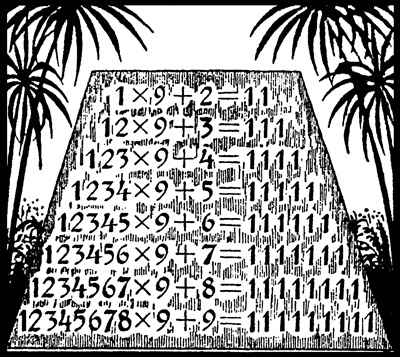
Как объяснить эти своеобразные результаты умножения, эту странную закономерность?

Решение

Возьмем для примера какой-нибудь из средних рядов нашей числовой пирамиды: 123456 x 9 + 7. Вместо умножения на 9 можно умножить на (10 - 1), т. е. приписать 0 и вычесть умножаемое:

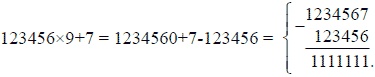
Достаточно взглянуть на последнее вычитание, чтобы понять, почему тут получается результат, состоящий только из одних единиц.

Мы можем понять это, исходя и из других рассуждений. Чтобы число вида 12345… превратилось в число вида 11111…, нужно из второй его цифры вычесть 1, из третьей - 2, из четвертой - 3, из пятой - 4 и т. д.; иначе говоря, вычесть из него то же число вида 12345…, лишенное своей последней цифры, - т. е. вдесятеро уменьшенное и предварительно сокращенное на последнюю цифру. Теперь понятно, что для получения искомого результата нужно наше число умножить на 10, прибавить к нему следующую за последней цифру и вычесть из результата первоначальное число (а умножить на 10 и отнять множимое - значит, умножить на 9).

Задача № 35

Сходным образом объясняется образование и следующей числовой пирамиды, получающейся при умножении определенного ряда цифр на 8 и прибавлении последовательно возрастающих цифр. Особенно интересна в этой пирамиде последняя строка, где в результате умножения на 8 и прибавления 9 происходит превращение полного натурального ряда цифр в такой же ряд, но с обратным расположением.

Попытайтесь объяснить эту особенность.

Решение

Получение таких странных результатов уясняется из следующей строки:

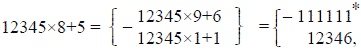
* Почему 12345 x 9 + 6 дает именно 111111, было показано при рассмотрении предыдущей числовой пирамиды.

то есть 12345 x 8 + 5 = 111111 - 12346. Но вычитая из числа 111111 число 12346, составленное из ряда возрастающих цифр, мы, как легко понять, должны получить ряд убывающих цифр 98765.

Задача № 36

Вот, наконец, третья числовая пирамида, также требующая объяснения:

Решение

Эта пирамида есть прямое следствие первых двух. Связь устанавливается очень легко. Из первой пирамиды мы знаем уже, что, например:

12345 x 9 + 6 = 111111.

Умножив обе части на 8, имеем:

(12345 x 8 x 9) + (6 x 8) = 888888.

Но из второй пирамиды мы знаем, что

12345 x 8 + 5 = 98765, или 12345 x 8 = 98760.

Значит:

888888 = (12345 x 8 x 9) + (6 x 8) = (98760 x 9) + 48 = (98760 x 9) + (5 x 9) + 3 = (98760 + 5) x 9 + 3 = 98765 x 9 + 3.

Вы убеждаетесь, что оригинальные числовые пирамиды не так уже загадочны, как кажутся с первого взгляда. Курьезно, что мне случилось как-то видеть их напечатанными в одной немецкой газете с припиской: «Причина такой поразительной закономерности никем еще до сих пор не была объяснена»…

Девять одинаковых цифр

Задача № 37

Конечная строка первой из сейчас (стр. 215) рассмотренных «пирамид»:

12345678 x 9 + 9 = 111111111

представляет образчик целой группы интересных арифметических курьезов, собранных в нашем музее в следующую таблицу:

Откуда такая закономерность в результатах?

Решение

Примем во внимание, что

12345678 x 9 + 9 = (12345678 + 1) x 9 = 12345679 x 9.

Поэтому

12345679 x 9 = 111111111.

А отсюда прямо следует, что

12345679 x 9 x 2 = 222222222

12345679 x 9 x 3 = 333333333

12345679 x 9 x 4 = 444444444 и т. д.

Цифровая лестница

Задача № 38

Что получится, если число 111111111, с которым мы сейчас имели дело, умножить само на себя? Заранее можно предвидеть, что результат должен быть диковинный, - но какой именно?