Читать книгу - "Битва при черной дыре. Мое сражение со Стивеном Хокингом за мир, безопасный для квантовой механики - Леонард Сасскинд"

Принцип неопределенности стал тем перевалом, который поделил физику на доквантовую классическую эпоху и постмодернистскую эру квантовых «странностей». Классическая физика охватывает все, что появилось до квантовой механики, включая ньютоновскую теорию движения, максвелловскую теорию света и эйнштейновскую теорию относительности. Классическая физика детерминистична; квантовая физика полна неопределенности.

Принцип неопределенности — это странное и дерзкое утверждение, сделанное в 1927 году 26-летним Вернером Гейзенбергом, после того как он и Эрвин Шрёдингер открыли математику квантовой механики. Даже в эпоху множества необычных идей этот принцип выглядит крайне странным. Гейзенберг не утверждал, что есть какие-либо ограничения на точность, с которой можно измерить положение объекта. Координаты, задающие положение частицы в пространстве, можно определить с любой желаемой степенью точности. Он также не ставил пределов точности, с которой может быть измерена скорость объекта. Но он утверждал, что никакой эксперимент, как бы сложно и изобретательно он ни был поставлен, не может измерить положение и скорость одновременно. Это как если бы эйнштейновский Бог устроил бы все так, чтобы никто и никогда не мог предсказывать будущее.

Хотя принцип неопределенности посвящен расплывчатости, но в нем самом, парадоксальным образом, нет ничего расплывчатого. Неопределенность — это строгая концепция, включающая измерения вероятностей, интегральное исчисление и прочие математические изыски. Впрочем, перефразируя широко известное выражение, одна картинка стоит тысячи уравнений. Начнем с представления о распределении вероятностей. Пусть для очень большого числа частиц, скажем для триллиона, изучается их расположение вдоль горизонтальной оси, также называемой осью X. Первая частица оказалась в точке х = 1,3257, вторая—х = 0,9134 и т. д. Можно составить длинный список координат всех частиц. К сожалению, этот список займет около десяти миллионов книг вроде этой, и для большинства задач в нем не будет чего-то особенно интересного. Было бы куда информативнее получить статистический график, показывающий долю частиц, обнаруженных на каждом значении х. Этот график может выглядеть примерно так:

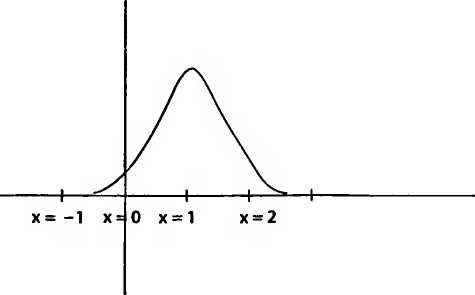
Один взгляд на этот график говорит нам, что большинство частиц находится вблизи точки х = 1. Для некоторых задач этого может хватить. Но достаточно чуть присмотреться, чтобы высказаться значительно точнее. Около 90 % частиц находятся между отметками х = 0 и х = 2. Если делать ставки на то, где окажется конкретная частица, то наибольшие шансы будут при х— 1, но неопределенность — математическая мера того, насколько «широка» кривая на графике, — составит около 2 единиц^[48]. Греческая буква дельта (Δ) служит стандартным математическим обозначением для неопределенности. В данном случае Ах означает неопределенность координаты х для рассматриваемых частиц.

Проделаем еще один мысленный эксперимент. Вместо измерения положений частиц будем измерять их скорости, считая их положительными для частиц, движущихся вправо, и отрицательными для тех, что движутся влево. На этот раз горизонтальная ось представляет скорость V.

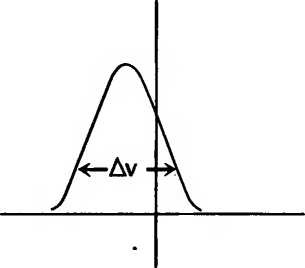
Из графика видно, что большинство частиц движется влево, и можно также составить представление о разбросе скоростей Δν.

Принцип неопределенности говорит примерно следующее: любая попытка уменьшить неопределенность положения неизбежно будет приводить к увеличению неопределенности скорости. Например, можно целенаправленно выбрать только частицы в узком диапазоне значений х: скажем, между х = 0,9 и х = 1,1, отбросив все остальные. Для этого тщательно отобранного подмножества частиц неопределенность будет составлять всего 0,2, в десять раз меньше исходного Δх. Можно надеяться таким способом обойти принцип неопределенности, но это не срабатывает.

Оказывается, если взять то же подмножество частиц и измерить их скорости, разброс их значений окажется значительно больше, чем в исходной выборке. Вы можете удивиться, почему так происходит, но, боюсь, это просто один из непостижимых квантовых фактов, которым нельзя дать классического объяснения. Это одна из тех вещей, о которых Фейнман говорил: «Теоретическая физика отказалась от этого».

При всей непостижимости, это экспериментальный факт: всякий раз, когда мы сокращаем Δх, неизбежным следствием становится рост Δv. И аналогично, все, что приводит к сокращению Δv, вызывает увеличение Δх. Чем сильнее мы стараемся зафиксировать положение частицы, тем неопределеннее мы делаем ее скорость, и наоборот.

Это было грубое описание идеи, но Гейзенберг смог выразить свой принцип неопределенности в более точной, количественной форме. Он утверждает, что произведение Δν, Δх и массы частицы т всегда больше (>) постоянной Планка h.

mΔvΔx > h.

Посмотрим, как это работает. Предположим, что мы очень тщательно подготовили частицы, так что величина Δх чрезвычайно мала. Это вынуждает неопределенность скорости Δν становиться достаточно большой, чтобы произведение было больше h. Чем меньше мы делаем Δх, тем больше становится Δν.

Как получается, что мы не замечаем проявлений принципа неопределенности в повседневной жизни? Разве бывало такое, чтобы при вождении автомобиля наше положение становилось «размытым», при внимательном взгляде на спидометр? И разве спидометр сходит с ума, когда мы определяем по карте, где именно мы находимся? Конечно нет. Но почему? Ведь принцип неопределенности никому не делает поблажек, он применим ко всему, в том числе к вам и вашему автомобилю, точно так же как к электронам. Ответ связан с массой, которая входит в формулу, и с малостью постоянной Планка. В случае электрона очень малая масса электрона сокращается с малостью h, и потому совокупная неопределенность Δν и Δх должна быть весьма значительной. Но масса автомобиля очень велика в сравнении с постоянной Планка. Поэтому обе величины Δν и Δх могут оставаться неизмеримо малыми, не нарушая принципа неопределенности. Теперь понятно, почему природа не приспособила наш мозг к квантовой неопределенности. В этом не было необходимости: в обыденной жизни мы никогда не сталкиваемся с объектами достаточно легкими, чтобы приходилось учитывать принцип неопределенности.