Читать книгу - "Число, пришедшее с холода. Когда математика становится приключением - Рудольф Ташнер"

С изобретением степеней математика получила в свое распоряжение очень мощный инструмент обозначения чисел, которые немыслимо получать с помощью умножения, не говоря уже о сложении. Дело в том, что степень тоже можно возвести в степень, получив так называемую степенную башню, например

5^4³

Для начала надо заметить, что существует два способа прочтения этой степенной башни. При первом из них сначала возводят пять в четвертую степень и получают 625, а затем это число возводят в третью степень, то есть 625³ = 244 140 625. В этом случае результат представляют как

(5⁴)³ = 625³ = 244 140 625.

Другой способ представления этого числа заключается в том, что сначала вычисляют выражение 4³, равное 64, а затем возводят в 64-ю степень число 5, то есть вычисляют величину степени 5⁶⁴. Это число, начинающееся с цифр 5421… и содержащее 45 разрядов. В этом случае со степенной башней поступают так:

5^(4³) =

= 542 101 086 242 752 217 003 726 400 434 970 855 712 890 625.

Если степенную башню пишут без скобок, то имеют в виду второе из упомянутых выше прочтений. Другими словами, со степенями «работают» справа налево и сверху вниз. Так договорились делать не только потому, что такое прочтение при вычислении приводит к большему результату, а прежде всего потому, что первое прочтение, вообще говоря, не требует написания степеней в виде башни. В самом деле, например, выражение

(5⁴)³ = 5⁴ × 5⁴ × 5⁴ = 5^{4 + 4 + 4} = 5^{4 × 3}

в точности соответствует старому школьному правилу: для того чтобы возвести в степень число, выраженное степенью, надо перемножить показатели степени.

Самое большое число, которое можно записать всего тремя цифрами, выглядит так:

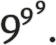
Это степенная башня, состоящая из трех девяток. Это число начинается с 4281… и содержит 369 693 100 разрядов.

Профессор информатики Стэнфордского университета Дональд Кнут заменил придуманный Брадвардином способ записи степеней новой символикой, которая лучше подходит для программирования, выполняемого обычным текстом. Например, степень 3² Кнут предложил записывать так: 3↑2. Вертикальная стрелка словно заменяет команду считать следующее число показателем степени. Таким же способом, как открыл Кнут, можно сокращенно записывать и степенные башни. Например, символами 3↑↑2 записывают степенную башню, состоящую из двух чисел 3. Это означает 3↑↑2 = 3↑3 = 3³ = 27. Здесь пока не заметно ничего особенного, но хитрость таится в самой записи двух вертикальных стрелок! Ибо 3↑↑3 — это уже степенная башня, состоящая из трех троек, то есть

3↑↑3 = 3↑3↑3 = 3^3³ = 3²⁷ = 7 625 597 484 987,

а 3↑↑4 — это степенная башня, состоящая из четырех троек, то есть

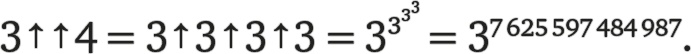
Этот числовой великан начинается с 1258… и содержит 3 638 334 640 025 разрядов, то есть он больше числа, записанного в виде степенной башни из трех девяток, которая с помощью метода Кнута записывается так: 9↑↑3.

Мало того, Кнут расширил свое обозначение еще на один шаг. Если он помещал между двумя числами три вертикальные стрелки, то число, стоящее справа от тройной стрелки, говорило, сколько раз надо было записать число, стоящее слева, и поставить между ними двойные стрелки. В этом случае с записью Кнута работают, как со степенной башней — то есть справа налево. Например, запись 3↑↑↑2 есть сокращенная запись 3↑↑3. Это число мы с грехом пополам еще можем себе представить — 7 625 597 484 987. Но, например,

3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑7625597484987.