Читать книгу - "Алекс в стране чисел. Необычайное путешествие в волшебный мир математики - Алекс Беллос"

Прежде чем продолжать чтение, рассмотрим два квадрата. Квадрат А по размеру равен квадрату В, и все прямоугольные треугольники внутри этих двух квадратов тоже имеют одинаковые размеры. Поскольку квадраты равны, площади белых областей внутри них тоже равны. Заметим теперь, что большой белый квадрат внутри квадрата А — это квадрат, построенный на гипотенузе прямоугольного треугольника. А меньшие белые квадраты внутри квадрата В — это квадраты, построенные на двух других сторонах треугольника. Другими словами, квадрат гипотенузы равен сумме квадратов двух других сторон. Готово.

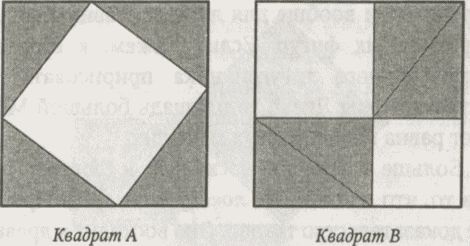
Поскольку мы можем построить квадраты, аналогичные А и В, для прямоугольного треугольника любой формы и размера, теорема должна быть верна во всех случаях.

Захватывающая увлекательность математики коренится в моменте внезапного проявления истины в доказательствах, подобных приведенному выше, когда все вдруг становится ясным. И тогда испытываемое интеллектуальное удовольствие граничит с физическим. В XII столетии это доказательство так потрясло индийского математика Бхаскару, что под иллюстрирующим его рисунком он в своей математической книге «Лиливати» вместо объяснений написал всего одно слово: «Зри!»

* * *

Имеется много других доказательств теоремы Пифагора; одно, особенно милое, приведенное на рисунке, приписывается арабскому математику Аннаиризи, а появилось оно около 900 года. Теорема там извлекается из повторяющегося узора. Улавливаете? (Если нет, то помощь можно почерпнуть в приложении 1 на веб-сайте, посвященном этой книге.)

В книге «Пифагорово предложение» Элиша Скотта Лумиса, изданной в 1940 году, приведено 371 доказательство этой теоремы. Их авторы были на редкость несхожие между собой люди; к примеру, одно доказательство в 1888 году предложила слепая девушка Эмма Кулидж; второе, в 1938 году — Энн Кондит, 16-летняя старшеклассница; авторами других считаются Леонардо да Винчи и американский президент Джеймс А. Гарфилд, правивший страной с марта по сентябрь 1881 года. Гарфилд наткнулся на свое доказательство во время математических развлечений с коллегами в бытность свою конгрессменом от Республиканской партии. «Мы рассматриваем его как нечто, по поводу чего члены обеих палат могут проявить единство, невзирая на партийные различия», — сказал он, когда его доказательство впервые было опубликовано в 1876 году.

Разнообразие доказательств — свидетельство жизненной силы математики. Нет и никогда не было одного-единственного «правильного» способа решения математической задачи, и исключительно интересно наблюдать, какими различными путями различные умы добирались до желанного решения. Возьмем, например, три доказательства теоремы Пифагора из трех различных эпох: одно предложил Лю Хуэй — китайский математик, живший в III веке, другое — Леонардо да Винчи, один из титанов эпохи Возрождения, а третье (в 1917 году) — Генри Дьюдени, самый знаменитый британский изобретатель головоломок. И Лю Хуэй, и Дьюдени дали «доказательства путем разбиения», в которых два малых квадрата разбиваются на фигуры, которые можно собрать в точности в большой квадрат. Вы можете пожелать изучить их доказательства, чтобы понять, как это делается. Доказательство Леонардо более необычно и требует большего напряжения мысли. (Если потребуется помощь, загляните на веб-сайт www.alexbellos.com.)

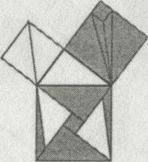
лю Хуэй

Генри Дьюдени

Леонардо да Винчи

Особо динамичное доказательство придумал в начале XX века нью-йоркский профессор математики Герман фон Баравалле. На рисунке показано, как большой квадрат, подобно амебе, делится на два меньших. Затемненные участки сохраняют свою площадь на каждом шаге. На шаге 4 два параллелограмма «скашиваются» за пределы области, а далее на шаге 5 эти параллелограммы преобразуются в квадраты, и — зри! — теорема доказана.

Доказательство Баравалле подобно наиболее общепринятому в математической литературе — тому, которое пошло от Евклида (около 300 года до н. э.).

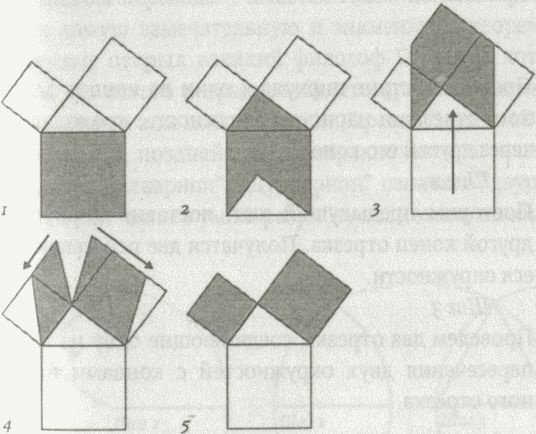
Доказательство теоремы Пифагора, предложенное Германом фон Баравалле

Евклид — самый знаменитый греческий математик после Пифагора — жил в Александрии. В его шедевре «Начала» содержится 465 теорем, которые отражали объем знаний, доступных грекам того времени. Греческая математика почти целиком состояла из геометрии — слово это происходит от греческих слов, означавших «земля» и «измерение»,— хотя содержание «Начал» и не имело отношения к устройству реального мира. Евклид действовал в абстрактном мире точек и линий. Средства, которыми он разрешал себе пользоваться, представляли собой лишь карандаш, линейку и циркуль, — по каковой причине именно они стали основным содержимым детских пеналов на протяжении столетий.

Первая задача Евклида — книга 1, предложение 1 — состояла в том, чтобы показать, что по любому заданному отрезку можно построить равносторонний треугольник (то есть треугольник с тремя равными сторонами), причем со стороной, равной заданному отрезку. Он использовал следующий метод: