Читать книгу - "Популярная физика. От архимедова рычага до квантовой теории - Айзек Азимов"
Аннотация к книге "Популярная физика. От архимедова рычага до квантовой теории - Айзек Азимов", которую можно читать онлайн бесплатно без регистрации
Каким же образом можно сложить отдельные движения и получить результирующую этих движений? Это может быть сделано при помощи векторного сложения, по методу, наиболее легко представляемому в геометрической форме. Рассмотрим два движения в различных направлениях, эти два направления находятся под углом α друг к другу. (Символ α — греческая буква «альфа». Греческие буквы вообще часто используются в физике в качестве символов, чтобы ослабить нагрузку на обычные буквы алфавита.) Эти два движения могут тогда быть представлены двумя стрелками, находящимися под углом α, а длина этих двух стрелок пропорциональна соответствующим им скоростям. (Если одна скорость вдвое больше другой, то и соответствующая стрелка в два раза больше другой.) Если мы представим эти две стрелки как стороны параллелограмма, то результирующее движение, созданное из двух составляющих движений, может быть диагональю этого параллелограмма, которая находится в промежутке между направлениями составляющих компонентов.
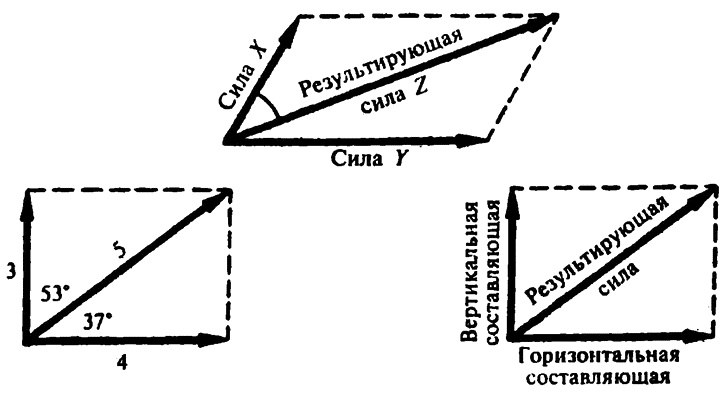
Параллелограмм сил
Зная значения этих двух скоростей и угла между ними, можно вычислить значение и направление результирующей скорости даже и без геометрических построений, хотя последние всегда полезны в качестве зрительной помощи. Например, если одна скорость — 3 м/с в одном направлении, а другая — 4 м/с в направлении перпендикулярном (под прямым углом к) первому, то результирующая скорость — 5 м/с, в направлении, которое составляет угол менее чем 37° с большим компонентом и более чем 53° — с меньшим.
Таким же образом данная конкретная скорость может быть разложена на две составляющие скорости. Если мы выразим данную скорость как диагональ параллелограмма, то две из смежных сторон параллелограмма представят собой составляющие скорости. Это может быть проделано бесконечное число раз, так как линия, представляющая скорость или силу, может быть представлена диагональю бесконечного числа параллелограммов. Однако удобно, чтобы скорость была разложена на компоненты, которые находятся под прямыми углами друг к другу. В этом случае параллелограмм превращается в прямоугольник.
Этот метод использования параллелограмма может применяться для сложения или разложения любого количества векторов. Данный метод очень часто используется для расчета сил, и поэтому обычно его называют «параллелограммом сил».
Теперь позвольте нам вернуться к Луне. Относительно Земли она двигается по эллиптической орбите. Однако эллипс, который она описывает в своем вращении вокруг Земли, очень близок по форме к кругу. Луна путешествует по этой орбите со скоростью, которая близка к постоянной.
Хотя линейная скорость Луны почти постоянна, ее векторная скорость, конечно, — нет. Так как Луна перемещается по кривой, направление ее движения в каждый данный момент времени изменяется, и поэтому ее векторная скорость изменяется тоже. Если мы говорим, что векторная скорость Луны непрерывно изменяется, то, конечно, должны сказать, что она подвергается постоянному ускорению.
Если же мы рассматриваем Луну как перемещающуюся с постоянной скоростью по равномерно круговому пути (что является, по крайней мере приблизительно, истинным), то мы можем сказать, что в каждую последовательную единицу времени направление ее движения изменяется на одну и ту же величину. Поэтому она испытывает постоянное ускорение и, согласно второму закону движения Ньютона, должна быть подчинена воздействию постоянной силы. Поскольку изменение в направлении движения всегда направлено к Земле, то ускорение и соответственно сила тоже должны быть направлены к Земле.
Конечно, если имеется сила, притягивающая Луну к Земле, это может быть та же хорошо известная сила, которая притягивает яблоко к земле. Однако, если это было бы так и Луна испытывала бы постоянное ускорение, направленное к Земле при наличии постоянной силы, почему же она не падает на Землю, как делает яблоко?
Чтобы понять, почему этого не происходит, мы должны разложить движение Луны на две составляющие движения, находящиеся под прямым углом друг к другу. Одна из составляющих направлена как стрелка, указывающая на Землю, по радиусу круговой орбиты Луны. Она представляет собой движение в ответ на силу, притягивающую Луну к Земле. Другая составляющая направлена под прямым углом к первой и, таким образом, представляет собой касательную к кругу орбиты Луны. И Луна бы двигалась по касательному движению, если бы не имелось никакой силы, притягивающей ее к Земле. Фактическое же движение лежит между этими двумя составляющими. Луна, другими словами, всегда падает на Землю, но в то же самое время также «отступает в сторону».
В некотором смысле это «отступление» означает, что поверхность Земли отходит от Луны с такой же скоростью, как Луна приближается к ней, падая. Таким образом, расстояние между Землей и Луной остается неизменным. Чтобы было более понятно, представим себе снаряд, выстреленный горизонтально с вершины горы на земле, и развивающий все большую и большую скорость. Чем больше скорость, тем дальше перемещается снаряд, прежде чем удариться о землю. Чем дальше он перемещается, тем дальше от него сферическая земная поверхность, таким образом увеличивается перемещение снаряда. Ну и наконец, если снаряд выстрелен вперед с достаточной скоростью, высота его падения становится равной величине кривизны земной поверхности, и снаряд «остается на орбите». Именно так на орбиту Земли выводят искусственные спутники, и именно поэтому Луна не падает на Землю, а остается на орбите.
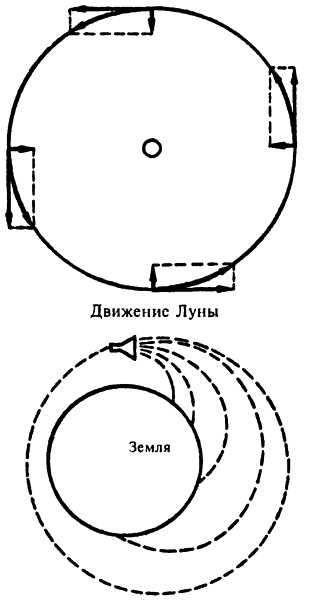
«На орбите»
При рассмотрении движения Луны мы должны учитывать только ту составляющую движения, которая направлена к Земле. Естественно возникает вопрос: не является ли этот компонент результатом действия той же силы, которая притягивает к земле яблоко? Ну что же, давайте обратимся к яблоку и посмотрим, как интерпретировать силу взаимодействия между ним и землей в свете законов движения.
Во-первых, все яблоки падают с одним и тем же ускорением, независимо от того, насколько они массивны. Но если одно яблоко имеет массу вдвое большую, чем второе яблоко, и все же падает с тем же самым ускорением, то на первое яблоко должна воздействовать вдвое большая сила (согласно второму закону движения). Сила, притягивающая яблоко к земле (часто ее называют весом яблока), должна быть пропорциональна массе яблока.
Но согласно третьему закону движения всякий раз, когда одно тело прикладывает силу к другому, второе прикладывает равную и противоположную силу к первому. Это означает, что, если Земля привлекает яблоко с некоторой нисходящей силой, яблоко привлекает Землю с равной восходящей силой.
Это кажется странным. Как крошечное яблоко может проявлять силу, равную той, что проявлена огромной Землей? Если бы это происходило, то можно было бы ожидать, что яблоко притянет к себе другие объекты, как это делает Земля, но этого, конечно, не происходит. Логично было бы объяснить это предположением, что сила притяжения между яблоком и землей зависит не только от массы яблока, но также и от массы Земли. Она не может зависеть от суммы масс, поскольку, когда мы удвоим массу яблока, суммарная масса яблока и Земли остается примерно прежней, в то время как сила притяжения удваивается. Очевидно, что она должна зависеть не от суммы масс, а от произведения масс.
Прочитали книгу? Предлагаем вам поделится своим впечатлением! Ваш отзыв будет полезен читателям, которые еще только собираются познакомиться с произведением.
Оставить комментарий
-
 Ольга18 февраль 13:35
Измена .не прощу часть первая закончилась ,простите а где же вторая часть хотелось бы узнать
Измена. Не прощу - Анастасия Леманн
Ольга18 февраль 13:35
Измена .не прощу часть первая закончилась ,простите а где же вторая часть хотелось бы узнать
Измена. Не прощу - Анастасия Леманн
-
 Илья12 январь 15:30
Книга прекрасная особенно потому что Ее дали в полном виде а не в отрывке
Горький пепел - Ирина Котова
Илья12 январь 15:30
Книга прекрасная особенно потому что Ее дали в полном виде а не в отрывке
Горький пепел - Ирина Котова
-
 Гость Алексей04 январь 19:45
По фрагменту нечего комментировать.
Бригадный генерал. Плацдарм для одиночки - Макс Глебов
Гость Алексей04 январь 19:45
По фрагменту нечего комментировать.
Бригадный генерал. Плацдарм для одиночки - Макс Глебов
-
 Гость галина01 январь 18:22
Очень интересная книга. Читаю с удовольствием, не отрываясь. Спасибо! А где продолжение? Интересно же знать, а что дальше?
Чужой мир 3. Игры с хищниками - Альбер Торш
Гость галина01 январь 18:22
Очень интересная книга. Читаю с удовольствием, не отрываясь. Спасибо! А где продолжение? Интересно же знать, а что дальше?
Чужой мир 3. Игры с хищниками - Альбер Торш





