Читать книгу - "Число, пришедшее с холода. Когда математика становится приключением - Рудольф Ташнер"

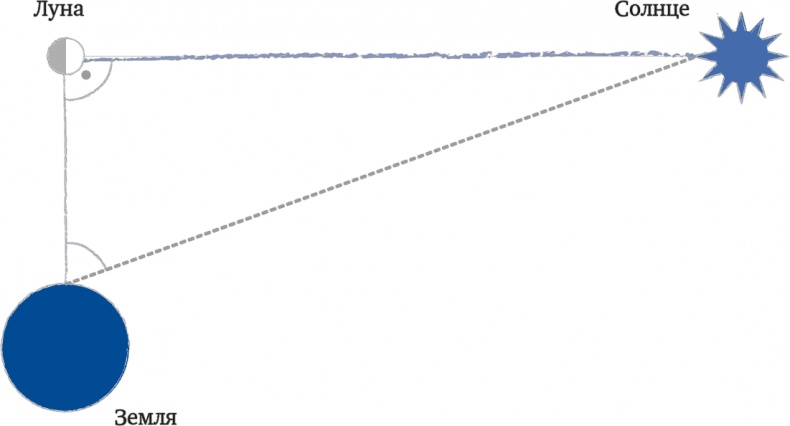
Рис. 4. Принцип измерения расстояния от Земли до Солнца по Аристарху: когда Луна освещена в точности наполовину, направление зрительного луча от Земли до Луны составляет прямой угол с направлением зрительного луча, направленного от Луны к Солнцу. Если теперь измерить угол между лучом, соединяющим Землю и Луну, и лучом, соединяющим Землю и Солнце, то можно получить углы прямоугольного треугольника. Исходя из известной длины одной стороны этого треугольника и его углов, можно посчитать, во сколько раз расстояние от Земли до Солнца превышает расстояние от Земли до Луны. Правда, измеренный угол между направлениями от Земли до Луны и от Земли до Солнца настолько близок к прямому, что Аристарх не смог получить достоверные данные

Теоретически метод Аристарха безупречен. Но при попытке его практического применения он оказывается невыполнимым. Угол между направлением зрительной оси от Земли до Луны и направлением зрительной оси от Земли до Солнца очень мало отличается от прямого. Аристарх не мог измерить эту разницу с помощью доступных ему методов измерения углов. Направления лучей от Солнца до Луны и от глаза до Солнца оказывались практически параллельными. Таким образом, ясно, что Солнце находится от Земли на расстоянии, многократно превышающем расстояние от Земли до Луны. Аристарх считал, что в девятнадцать раз. Однако он сильно ошибся. Солнце располагается от Земли дальше, чем Луна, приблизительно в 400 раз.

Это расстояние приблизительно равно 150 миллионам километров. Произнести число 150 миллионов легко, но едва ли нам удастся вообразить себе такое расстояние наглядно. Достаточно ли сказать, что надо обогнуть Землю 3750 раз, чтобы преодолеть это немыслимо огромное расстояние? Или вспомнить о том, что свету, который каждую секунду преодолевает 300 тысяч километров, требуется около восьми минут для того, чтобы преодолеть расстояние от Солнца до Земли? Все это соответствует действительности, но превосходит силу нашего воображения.

Но с удаления от Земли до Солнца астрономические расстояния только начинаются. Самые близкие к нам звезды расположены от нас в 250 тысяч раз дальше, чем Солнце. Это приблизительно 40 триллионов километров. Свет в течение одного года преодолевает расстояние, равное девяти с половиной триллионам километров, и именно это расстояние для краткости очень мило называют «световым годом». Это необходимое сокращение, ибо, например, Млечный Путь, этот звездный остров, составленный из миллиардов звезд, одной из которых является наше Солнце, имеет диаметр около ста тысяч световых лет. Этот звездный остров называется галактикой. Ближайшая следующая галактика — туманность Андромеды. Она удалена от нас на расстояние около двух миллионов световых лет, но в ясную звездную ночь ее можно различить на небосводе невооруженным глазом в виде расплывчатой светящейся точки. В привычных единицах измерения это расстояние соответствует более чем 18 квинтиллионам километров — числу, напоминающему число зернышек риса из рассказа о мудреце и магарадже.

Но и это всего лишь начало рассказа космологов о величине мирового пространства. В нем таких галактик, таких звездных островов, как Млечный Путь или туманность Андромеды, насчитывается больше 100 миллиардов. С помощью мощнейших наземных телескопов и телескопов, установленных на искусственных спутниках Земли, астрономы наблюдают немыслимые бездны мироздания. Теоретически с помощью этих устройств можно проникнуть взором на расстояние почти 50 миллиардов световых лет, а дальше начинается «горизонт событий Вселенной», за который, если верить общей теории относительности Эйнштейна, мы не можем заглянуть даже с помощью самой совершенной аппаратуры. Если выразить 50 миллиардов световых лет в километрах, то получается число 450 секстиллионов километров.

Опять-таки произнести это легко, но наглядно представить невозможно.